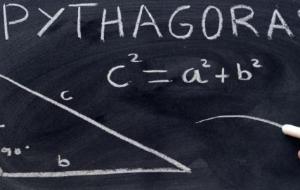رياضيات

كتلة لتر الماء الكثافة تساوي الكتلة/الحجم، وعليه يمكن حساب كتلة الماء عند معرفة حجمه اعتماداً على كثافته عند درجة الحرارة تلك؛ حيث تكون كثافة الماء أكبر ما يمكن عند درجة حرارة 4 درجة سيليسيوس، أو 39.2 فهرنهايت؛ بينما تقل عند ارتفاع درجة الحرارة أو انخفاضها عن ذلك؛ فكثافة الماء تختلف باختلاف درجة الحرارة، وعند درجة الحرارة 4 درجة سيليسيوس تكون كثافة الماء 1 كيلوغرام/لتر؛ أي أنّ كتلة 1 لتر من الماء عند درجة الحرارة هذه تساوي 1 كيلوغرام أو 2.2 باوند تبعاً للنظام الإمبراطوري، كما أنّ كتلة 1

مقدار اللتر تتم في النظام المتري إضافة بادئات إلى جميع وحداته الأساسية؛ لمعرفة قيمة الوحدات المحتلفة الأخرى بمجرد النظر إلى بدايتها، والأمر ذاته ينطبق على اللتر الذي يعتبر الوحدة الأساسية لقياس الحجم في النظام المتري، وذلك كما في الجدول الآتي: الوحدة قيمتها بالنسبة للتر الكيلو لتر أكبر بنحو 1000 مرة من اللتر؛ أي 1 لتر = 10 كيلو لتر. الهكتو لتر أكبر بنحو 100 مرة من اللتر؛ أي 1 لتر = 10 هكتو لتر. الديكا لتر أكبر بنحو 10 مرات من اللتر؛ أي 1 لتر = 0.1 ديكا لتر. اللتر الوحدة الأساسية الديسي لتر

قانون عدد جهات أو وجوه الهرم الجانبية تًعرف الأسطح المسطّحة المكوّنة لأي شكل هندسي باسم الوجوه (بالإنجليزية: Faces)، وعندما يلتقي وجهان من أوجه الشكل الهندسي فإنّ الخط المتشكل بينهما يُعرف باسم الحافة (بالإنجليزية: Edge)، وتكون هذه الحواف مستقيمة، وغير منحنية، أما عند التقاء حافتين أو أكثر فيتكوّن في نقطة التقائهما ما يُعرف باسم الرأس، أو الزاوية (بالإنجليزية: Vertex)، ويكون عدد أضلاع القاعدة في الهرم دائماً مساوياً لعدد الأوجه الجانبية؛ فمثلاً الهرم الثلاثي له قاعدة ثلاثية لها ثلاثة أضلاع،

قوانين الاحتمالات هناك مجموعة من القوانين الخاصة بالاحتمالات، وهي: احتمالية وقوع الحادث = عدد عناصر الحادث/عدد عناصر الفضاء العيني (Ω)، والأمثلة الآتية توضّح ذلك: مثال: ما هو احتمال الحصول على العدد 4 عند رمي حجر النرد؟ عدد عناصر الحادث = 1 عدد عناصر الفضاء العيني = 6، وذلك لأن حجر النرد يتكون من (1، 2، 3، 4، 5، 6)، وهي النتائج الممكنة لهذه التجربة. احتمالية الحصول على العدد 4 = 1/6. مثال: يحتوي صندوق على 5 كرات، أربعة منها زرقاء، وواحدة حمراء، فما هو احتمال الحصول على كرة زرقاء عند سحب كرة

قسمة عدد على صفر إذا كان العدد لا يساوي صفر أ/0 إنّ قيمة ناتج قسمة أي عدد لا يساوي صفراً في الرياضيات على العدد صفر هي قيمة غير معرّفة (∞)؛ فلا يُوجَدُ جواب للسؤال الذي يُطرَح عن ناتج قسمة عدد ما على العدد صفر، وبالتالي فلا معنى للتعبير الرياضيّ الذي يعبّر عن القسمة على صفر، والذي يكون عادة على صورة 10/0 = ؟، أو 1/0 = ؟، أو حتى س/0= ؟؛ حيث يُعبِّر مفهومُ القسمة في الرياضيّات عن عمليّة تقسيم شيء ما على مجموعات، أو لعدّة أجزاء بشكلٍ متساوٍ؛ فعلى سبيل المثال في حالة الرغبة بتقسيم عشرين تفّاحةً

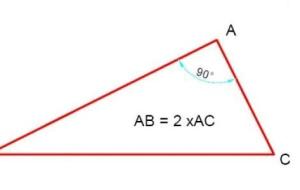
نص قانون نظرية فيثاغورس تنصّ نظرية فيثاغورس على أنّ: "'مجموع مربعي طولي ضلعي القائمة، وهما الضلعين الأقصر في المثلث قائم الزاوية مساوٍ لمربع طول الوتر وهو الضلع الأطول في المثلث'"، وبالرموز: نظريّة فيثاغورس= أ² ب²=ج²؛ حيث: أ، ب: ضلعا المثلث القائم أب ج. ج: وتر المثلث القائم أب ج، وهو الضلع الأطول فيه. ويجدر بالذكر هنا أن معكوس النظريّة أيضاً صحيح؛ حيث إن المثلث الذي تنطبق عليه نظريّة فيثاغورس، وهي: أ² ب²=ج²، هو بالضرورة مثلث قائم الزاوية. لمزيد من المعلومات والأمثلة حول المثلثات يُمكنك قراءة

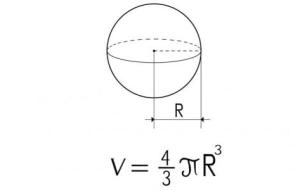
قانون مساحة سطح الكرة يُمكن تعريف مساحة سطح الكرة (بالإنجليزية: Surface area of a sphere) على أنه مقدار المساحة الإجمالية التي يشغلها سطح الكرة، ولإيجاد مساحة سطح الكرة يتم ضرب العدد (4) بالثابت باي، ثم ضرب الناتج بمربع نصف القطر، أي من خلال تطبيق المعادلة الآتية: مساحة سطح الكرة= 4×π×مربع نصف القطر، وبالرموز: م=4×π×نق²؛ حيث: م: مساحة سطح الكرة. نق: نصف قطر الكرة. π: باي، ثابت عددي قيمته 3.14 أو 22/7. فمثلاً لحساب مساحة سطح الكرة التي تبلغ قيمة نصف قطرها 5سم يُمكن تطبيق القانون كما يأتي: تعويض

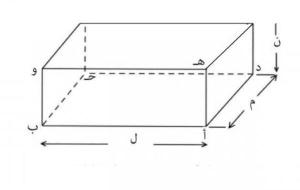
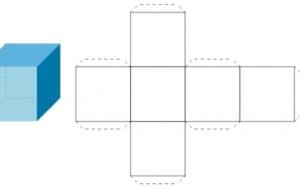
مساحة متوازي المستطيلات يحتوي متوازي المستطيلات على ستة أوجه، ويمكن حساب مساحته من خلال إيجاد مجموع مساحات هذه الأوجه، ولكن بما أن الأوجه المتقابلة في متوازي المستطيلات متطابقة، فإننا نحتاج إلى ثلاثة أوجه فقط للتعبير عن المساحة، باستخدام الأبعاد الثلاثية للتعبير عنها، وهي: الطول، والعرض، والارتفاع، وذلك كما يلي: مساحة متوازي المستطيلات الكلية= (2×الطول×العرض) (2×العرض×الارتفاع) (2×الطول×الارتفاع)، وبالرموز: مساحة متوازي المستطيلات= (2×أ×ب) (2×ب×ع) (2×أ×ع)؛ حيث: أ: طول متوازي المستطيلات. ب: عرض

قانون مساحة المكعب بما أن المكعب يتكون من أوجه مربعة الشكل، فمن المهم معرفة كيفية حساب مساحة المربع للتوصّل من خلالها إلى قانون مساحة المكعب. والمربع (بالإنجليزية: Square) هو شكل هندسي يُعد حالة خاصّة من المستطيل، إذ إنه مستطيلٌ جميع أضلاعه متساوية في الطول، ولإيجاد مساحة المستطيل يتم إيجاد حاصل ضرب الطول (الضلع الأطول) * العرض (الضلع الأقصر)، وبما أن أطوال أضلاع المربع متساوية فإن الطول يساوي العرض، وبالتالي يمكن الحصول على مساحة المربع بإيجاد حاصل ضرب الضلع في نفسه، أي بتربيعه، وبالرموز:

نظرة عامة حول المثلث متساوي الأضلاع يعتبر المثلث متساوي الأضلاع (بالإنجليزية: Equilateral Triangle) أحد أنواع المثلثات وفيه تكون فيه جميع الأضلاع متساوية في الطول، وجميع الزوايا متساوية في القياس ويساوي كل منها 60 درجة، ويساوي مجموع زوايا هذا المثلث 180 درجة كغيره من أنواع المثلثات. لمزيد من المعلومات حول المثلثات يمكنك قراءة المقال الآتي: أنواع المثلثات . قانون مساحة المثلث متساوي الأضلاع يمكن حساب مساحة المثلث متساوي الأضلاع باستخدام القانون العام لمساحة المثلث، وهو: مساحة المثلث=

محيط المثلث قانون حساب محيط المثلث يمكن تعريف المحيط (بالإنجليزية: Perimeter) بأنه الطول الكلي لحدود الشكل الهندسي التي تُحيط به من الخارج، ويُقاس المحيط بعدد من الوحدات الطولية مثل المتر (م)، والسنتيمتر (سم)، والمليمتر (مم)، ومحيط أي مثلث يُساوي مجموع أطوال أضلاعه، وبالتالي فإن: محيط المثلث متساوي الأضلاع = 3×أ، حيث أ: طول أحد اضلاع المُثلث. محيط المثلث متساوي الساقين = 2×أ ب، حيث أ: طول أحد الضلعين المُتساويين، وب: طول قاعدة المثلث. محيط المثلث مختلف الاضلاع = أ ب ج، حيث أ، وب، وجـ هي أطوال

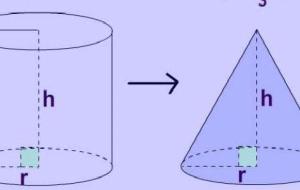
قانون المساحة الجانبية للإسطوانة يمكن تعريف الأسطوانة بأنها شكل ثلاثي الأبعاد مغلق، ويتكون من قاعدتين دائريتين، ومستطيل مُلتف حول القاعدة الدائرية، ويقع بين القاعدتين، وتجدر الإشارة إلى أن قاعدتي الأسطوانة متطابقتان، ومتوازيتان، وتعرف المساحة الجانبية للأسطوانة (بالإنجليزية: Cylinder Lateral Surface Area) بأنها مساحة جميع الوجوه باستثناء القاعدتين العلوية، والسفلية، أي أن المساحة الجانبية للأسطوانة هي مساحة السطح الذي يربط القاعدتين ببعضهما، ولفهم المساحة الجانبية يمكن تخيّل علبة لحفظ

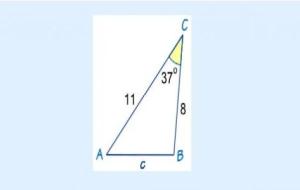
قانون الجيب ينصّ قانون الجيب (بالإنجليزية: Sine Law) على أنه: "نسبة طول أي ضلع في أيّ مثلث إلى جيب الزاوية المُقابلة له هي قيمة ثابتة ومُتساوية بالنسبة لجميع أضلاع المُثلث"، وهذا ينطبق على كُلّ أنواع المُثلثات وليس فقط المُثلثات القائمة الزاوية، ويُستخدم قانون الجيب عندما يُعرف قياس زاويتين وضلع واحد، أو ضلعين وزاوية غير محصورة بينهما، لإيجاد أضلاع وزوايا المثلثات القائمة وغير قائمة الزاوية، وتكون صيغة القانون على صورتين على النحو الآتي: أ/جا(أَ) = ب/جا(بَ) = ج/جا(جَ) ، أو جا(أَ)/أ = جا(بَ)/ب

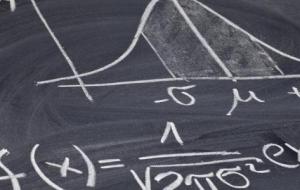
نظرة عامة حول التباين يُعرف التباين (بالإنجليزية: Variance) بأنه أحد مقاييس التشتت بين القيم لعينة ما، وهو يقيس مقدار تشتت القيم عن الوسط الحسابي، وعن بعضها البعض، ويُرمز له عادة بالرمز (σ)، وإذا كانت قيمة التباين كبيرة فإن هذا يعني أن القيم متباعدة عن بعضها، وعن الوسط الحسابي، وفي المقابل إذا كانت قيمته صغيرة فإن هذا يعني أن القيم متقاربة من بعضها، ومن الوسط الحسابي، أما إذا كانت قيمته صفر فإنّ هذا يعني أن القيم متماثلة، ومن الجدير بالذكر أن قيمة التباين تكون دائماً موجبة، وذلك لأن التباين

علم الرياضيات يعتبر علم الرياضيات أساس العلوم جميعها، وأساس تطورها ونجاحها، وهو المفتاح الذي من خلاله يتم الدخول إلى برهنة جميع النظريات والتطبيقات، وهو علم قديم جداً، بدأ وتطور نظراً لحاجة الناس للحساب والتعاملات الرياضية في جميع شؤون الحياة. كما تطور هذا العلم على يد مجموعةٍ كبيرةٍ من علماء الرياضيات العباقرة، الذين كان لهم الفضل الأكبر في اكتشاف النظريات، والقوانين، والبراهين جميعها، ومن الجدير بالذكر أنّ علم الرّياضيات دخل في العلوم جميعها، وأصبح جزءاً لا يتجزأ منها، ومن المعروف أن علم

طريقة ضرب الأعداد الكبيرة تعتبر عملية الضرب من العمليات الأساسية في الرياضيات، وهي تعبّر عن عملية تكرار جمع العدد لنفسه لعدد معيّن من المرات، وفيما يلي توضيح طريقة ضرب الأعداد الكبيرة: ترتيب العددين المراد ضربهما عمودياً، بحيث يتم وضع العدد الأكبر في الأعلى، والعدد الأصغر في الأسفل، مع مع مراعاة وضع آحاد العدد الأول تحت آحاد العدد الثاني، وعشرات العدد الأول تحت عشرات العدد الثاني، ومئات العدد الأول تحت مئات العدد الثاني، وهكذا. 2 5 1 8 5 ــــــــــــــــ ضرب آحاد العدد السفلي بكل أرقام العدد

طريقة القسمة في عملية القسمة يُسمّى العدد الذي يسبق إشارة القسمة (المقسوم)، أما العدد الذي يلي إشارة القسمة فهو (المقسوم عليه)؛ فمثلاً في المسألة: 10÷5 = 2 يُسمّى العدد 10 المقسوم، والعدد 5 المقسوم عليه، أما العدد 2 فهو الباقي، ويمكن التحقّق من صحة الحل عن طريق ضرب المقسوم عليه في ناتج القسمة، ثم إضافة الباقي لما سبق، وإذا كان العدد الناتج مساوياً للمقسوم يكون الحل صحيحاً؛ أي أنّ: المقسوم = (ناتج القسمة×المقسوم عليه) الباقي، وفيما يلي توضيح لكيفية القيام بعمليتي القسمة الطويلة، والقسمة

قانون حساب محيط الدائرة يمكن تعريف محيط الدائرة (بالإنجليزية: Circumference) بأنه المسافة المحيطة بالدائرة، ولإيجاد محيط الدائرة فإنّه يجب أولاً التطرّق للمفاهيم الآتية: قطر الدائرة: هو القطعة المستقيمة الواصلة بين أية نقطتين على محيط الدائرة مروراً بالمركز، وقطر الدائرة = 2×نصف القطر. نصف قطر الدائرة: هو القطعة المستقيمة الواصلة بين مركز الدائرة، وأية نقطة على محيطها، ونصف قطر الدائرة = قطر الدائرة/2. يمكن إيجاد محيط الدائرة باستخدام أحد القانونين الآتيين: محيط الدائرة = π×قطر الدائرة. محيط

مفهوم النسبة المئوية يُمكن تعريف النسبة المئوية (بالإنجليزية: Percent) بأنها النسبة التي يشكّل العدد مئة الجزء الثاني منها، وتعود كلمة النسبة المئوية في أصلها إلى الكلمة اللاتينية (Per Centum)، والتي تَعني لكل مئة، وعادة يُعبّر عنها رياضياً بالرمز (%)، ويمكن التعبير عنها كذلك بأشكال أخرى بعد تحويلها إلى كسور عادية أو عشرية؛ فعلى سبيل المثال يمكن كتابة النصف على شكل النسبة المئوية (50%)، أو العدد العشري (0.5)، أو الكسر العادي (1/2)، ومن الأمثلة الأخرى على النسب المئوية: 100%=100/100=1،

نظرة عامة حول المعدل يقع المعدل أو المتوسط الحسابي عادة بين أكبر وأقل قيمة لمجموعة من البيانات، وهو يمثّل القيمة الوسطى منها، أو التي تعبّر بشكل عام عنها، ويعتمد استخدام المعدل على طبيعة الهدف المراد تحقيقه من الدراسة التي تم استخدامه فيها؛ حيث يُستخدم المعدل أو المتوسط الحسابي في جميع نواحي الحياة تقريباً؛ فمثلاً يستخدم في النواحي الاقتصادية لحساب متوسط الإنتاج، و متوسط الأجور، ومتوسط التكلفة، و الصادرات، و الواردات، والاستهلاك، والأسعار، كما يُستخدم من الناحية الأكاديمية من قبل المؤسسات

عملية القِسمة في الرياضيات ، تُعتبر القسمة العمليّةَ الرابعة من العمليات الحسابية الأساسية بعد الجمع والطرح والضرب . ويُعبّر عنها بإشارة (÷) أو (/). والقسمة تعني تقسيم الشيء إلى أجزاء أو مجموعات متساوية. وللتمثيل على ذلك، لنفترض وجود (12) تفاحة يُراد تقسيمها بالتساوي على (4) أشخاص، فكم عدد التفاحات التي سيأخذها الشخص الواحد؟ الجواب (3) تفاحات، حيثُ إنّ (12 تفاحة/4 أشخاص=3 تفاحات/شخص)، فالقسمة هي العملية العكسية للضرب، والمثال التالي يوضّح ذلك: 3×4=12. 4×3=12. 12÷4=3. 12÷3=4. بعض قواعد قابلية

طريقة إيجاد المضاعف المشترك الأصغر الطريقة التقليدية: تعتبر هذه الطريقة من الطرق القديمة والبدائية، ويتم فيها العثور على المضاعف المشترك الأصغر عن طريق كتابة مضاعفات كل عدد من الأعداد على حدة على شكل قائمة، ثم إيجاد أصغر مضاعف مشترك بينها، ويصعب عادة إجراء هذه الطريقة إلا في حال كانت الأعداد صغيرة؛ فمثلاً لإيجاد المضاعف المشترك الأضغر بين العددين 4، و6، يجب أولاً كتابة مضاعفات كل عدد على حدة حتى العثور على أصغر مضاعف مشترك بينهما، والمثال الآتي يوضّح ذلك: مضاعفات العدد 4: 4، 8، 12، 16،

طريقة التحويل من السنتيمتر إلى المتر يعرف الطول بأنه المسافة الفاصلة بين نقطتين، ويُستخدم لقياسه العديد من الوحدات ومنها: السنتي متر: يرمز له بالرمز (سم)، وهو إحدى وحدات قياس الطول المستخدمة في النظام العالمي للوحدات (SI)، وهو الشكل الحالي للنظام المتري، و 1سم= 100/1م. المتر: يرمز له بالرمز (م)، وهو الوحدة الأساسية لقياس الطول في النظام العالمي للوحدات كما ذُكر سابقاً، ولذلك يعرف هذا النظام بالنظام المتري، و 1م = 100سم، وللتحويل من سنتيمتر إلى متر فإنه يتم استخدام القوانين الآتية: القيمة

طرق حل المعادلة التربيعية تُمثّل حلول المُعادلة التربيعيّة القيم التي تساوي عندها المعادلة صفراً، ويُطلق عليها أحياناً اسم الجذور (بالإنجليزية: Roots) أو الأصفار (بالإنجليزية: Zeros)، وغالباً ما يكون للمُعادلة التربيعيّة حلّان، ويُمكن إيجاد هذه الحلول باستخدام طرق عدة منها: التحليل إلى العوامل (بالإنجليزية: Factor the Quadratic). الصيغة العامة لحل المعادلة التربيعية (بالإنجليزية: Quadratic Formula). إكمال المُربع (بالإنجليزية: Complete the Square). الجذر التربيعي (بالإنجليزية: Square Root