رياضيات

طرق حل المعادلات الأسية المعادلات الأُسيّة التي لها نفس الأساس: هي المعادلة التي يكون فيها الأساس متساوياً على طرفي إشارة التساوي، ومن الأمثلة على ذلك 4 = 4 ، ويتم حلها من خلال استخدام الحقيقة التي تنص على أنه عندما تتساوى الأساسات فإن الأسس تتساوى تلقائياً، وبالرموز: إذا كانت المعادلة على الصورة أ = ب ، وكان أ=ب، فإن س=ص. ما هو ناتج حل المعادلة الأسية الآتية: 5 =5 ؟ بما أن الأساسات متساوية فإن الأسس تتساوى، وعليه: 3س=7س-2، وبحلها كالمعادلات الخطية بطرح (3س) من الطرفين، ينتج أن: 2 = 4س، ومنه:

حل المعادلات الجبرية عند حل المعادلات الجبرية تجب مراعاة الأمور الآتية: عند حل أي معادلة جبرية فإن الخطوة الأولى هي تجميع الحدود المتشابهة. يجب الحرص دائماً على إضافة، أو طرح نفس القيمة للطرفين عند حل المعادلات. للتخلص من الكسر فإنه يتم ضرب الطرفين بمقلوب الكسر. يجب الحرص دائماً على قسمة طرفي المعادلة بنفس العدد شريطة أن لا يكون مساوياً للصفر. في بعض الأحيان قد يتم تطبيق بعض الاقترانات على طرفي المعادلة لحلّها مثل تربيع الطرفين. في حال وجود قوس فإنه يتم توزيع الحدود على القوس قبل البدء في حل

الإحصاء الإحصاء هو علم من علوم الرياضيات المهمة، يعتمد الإحصاء على مجموعة من البيانات المتوفّرة التي يقوم بتلخيصها وتمثيلها واستنتاج نتائجها بغرض التنبؤ والاستنتاج وعمل نماذج، علم الإحصاء علم قديم جداً تمثل في العديد من المجالات كإحصاء عدد الجنود والأسلحة والمال والمحاصيل وعدد الأفراد ومع مرور الوقت تطور الإحصاء وظهرت العديد من الطرق له، يستخدم الإحصاء في العدد من المجالات السياسية والاجتماعية والاقتصادية فهو مهم للشركات والحكومات ورجال الأعمال. جمع البيانات الإحصائية إنّ أهمّ مرحلة في العملية

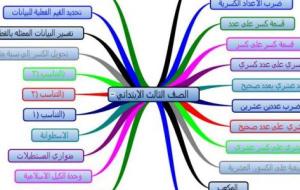
صعوبات تعلّم الرياضيات في المرحلة الابتدائية يعاني الطلبة في المرحلة الابتدائية صعوبات عديدة في تعلم الرياضيات، تتفاوت هذه الصعوبات بين الطلبة؛ بسبب تفاوت قدراتهم العقلية والفكرية، لذلك لا بدّ من الاهتمام بأسباب هذه الصعوبات، وطرق علاجها، من البديهيّ أنّ صعوبات التعلّم هي تحديات تواجه الطلبة تجعلهم غير قادرين على التواصل مع معلمي المادة، وغير قادرين أيضاً التجاوب مع نشاطات وفعاليات معلم الرياضيات خلال الدوام المدرسي، مما يجعلهم يعيشون في توتر، وقلق، وحالة من الإزعاج، وعدم الراحة. أسباب ضعف

نظرة عامة حول المتتابعات وأنواعها يمكن تعريف المتتاليات، أو المتتابعات (بالإنجليزية: Sequence) بأنها عبارة عن ترتيب لمجموعة من الأعداد التي تتبع عادة لنمط أو قاعدة محددة، ويمكن لهذه المتتالية أن تكون منتهية، أو غير منتهية. المتتابعات الحسابية يمكن تعريف المتتاليات الحسابية (بالإنجليزية: Arithmetic Sequences) بأنها المتتالية التي يكون الفرق بين كل حدين متتاليين من حدودها ثابت، ومن الأمثلة على المتتابعات الحسابية: 2، 4، 6، 8، 10، ......؛ حيث يمكن ملاحظة أنّ الفرق بين كلّ عددين متتاليين منها هو

نظرة عامة حول القوى في الرياضيات يمكن تعريف عملية رفع العدد للأسس أو القوى (بالإنجليزية: Exponents) بأنها العملية التي يتم فيها تكرار ضرب العدد المرفوع لقوة ما بنفسه، والذي يُعرف باسم الأساس لعدد معيّن من المرات يساوي قيمة القوة؛ فمثلاً أ = أ× أ × أ× أ×........ حتى تكرار العدد أ وهو الأساس بمقدار ن من المرات وهي الأس أو القوة؛ فمثلاً: 5 = 5×5×5، و 4 = 4×4×4، وتقرأ العدد أ مرفوعاً للقوة أو الأس ن. لمزيد من المعلومات حول حل المعادلات الأسية يمكنك قراءة المقال الآتي: طرق حل المعادلة الأسية . خواص

خصائص الاقتران الخطي للاقتران الخطي خصائص عديدة منها ما يلي: يتمثل مجال الاقتران الخطيّ ومداه بمجموعة الأعداد الحقيقيّة (ح). يحتوي الاقتران الخطيّ على مُتغيّرين فقط مرفوعين للأس واحد، وبالتالي فإنّ رسمه البياني يتمثل بخطّ مُستقيم كما ذُكر سابقاً. تُمثل جميع الأزواج المُرتبة (س، ص) الناتجة عن تعويض قيم مختلفة لـ س في معادلة الاقتران الخطيّ جميع النقاط الموجودة على الخط. يتمثل الميل دائماً بمُعدّل التغيّر للاقتران الخطيّ. تحتوي المُعادلة الخطيّة المكتوبة بصيغة الميل-القاطع على قيمة الميل والقيمة

نظرة عامة حول نظام المعادلتين المقصود بحل جملة معادلتين هو حل النظام المكوّن من معادلتين خطيتين تضمّ كل منهما متغيرين، وذلك بإيجاد قيم المتغيرين اللذين يحققان كِلتا المعادلتين معاً، ويمكن توضيح ذلك بأن قيم المتغيرين التي تمثّل حلّاً لمعادلة واحدة من المعادلتين ولا تحقّق المعادلة الثانية، لا تعدّ حلاً للنظام بأكمله، ويجدر بالذكر هنا أنّ حل نظام المعادلتين يمكن أنْ يكون على إحدى الصور الآتية: لنظام المعادلتين حل وحيد، أي أنّ هناك زوجاً واحداً يحقق كلتا المعادلتين (س،ص)، وهو يمثّل نقطة تقاطع

تعريف الخط المستقيم يمكن تعريف الخط المستقيم (بالإنجليزية: Straight Line) بأنه عبارة عن شكل هندسي مستقيم تماماً وغير منحنٍ، وليس له سُمك، وله بعد واحد فقط، ويمكن أن يمتد في أيٍّ من الاتجاهات إلى المالانهاية، ويتميز بأن له ميل ثابت، وتجدر الإشارة بأن الخط المستقيم يمثّل دائماً أقصر مسافة بين أي نقطتين، وهناك عدة أنواع من الخطوط، وذلك كما يلي: الخطوط العمودية: (بالإنجليزية: Vertical Straight Lines) هي الخطوط التي تمتد بشكل عمودي إما للأعلى، أو للأسفل. الخطوط الأفقية: (بالإنجليزية: Horizontal

التحويل بين وحدات الكتلة للتحويل بين وحدات الكتلة المختلفة فإنه يجب التعريف بالبادئات المختلفة المستخدمة في النظام العالمي للوحدات، والتي تساوي كل منها عند إضافتها للوحدة الأصلية (وهي الغرام في حالة وحدات الكتلة) الوحدة الأصلية بمقدار من مضاعفات العدد 10، وذلك كما يلي: البادئة قيمتها بالنظام العشري إكسا (exa) 10 بيتا 10 تيرا 10 جيجا 10 ميجا 10 كيلو 10 هكتو 10 ديكا 10 ديسي 10 سنتي 10 ميلي 10 ميكرو 10 نانو 10 بيكو 10 فيمتو 10 أتو 10 كما تمثّل الجداول الآتية وحدات الكتلة المختلفة، وكيفية التحويل

التقويم الهجري والميلادي للوقت والتاريخ أهمية بالغة في حياتنا العامة، ونرى أنَّ عدداً من الدول تعتمِدُ على التقويم الميلادي، وبعض الدول تعتمِدُ على التقويم الهجري وهذا الاختلاف بين الدول يستدعي معرفة طريقة التحويل بين التقويميين، وهي هذا المقال سنوضح الفرق بين التقويم الهجري والتقويم الميلادي وطريقة التحويل بينهما. التاريخ الهجري بدأ العمل بالتقويم الهجري في زمن الخليفة عمر بين الخطاب، ويعتّمدُ التقويم الهجري على العام الذي هاجر فيه الرسول محمد علية الصلاة والسلام من مكة المكرمة إلى المدينة

تحويل الوزن من كيلوغرام إلى باوند يُمكن تحويل وزن جسم ما من الكيلوغرام إلى الباوند من خلال الضرب بمعامل التحويل وهو 2.2 باوند، أي أنّ كل كتلة وزنها واحد كيلوغرام فإن وزنها بالباوند هو 2.2 باوند، والجدير بالذكر أنّ القيمة 2.2 هي قيمة تقريبية لتحويل الكيلوغرام إلى باوند، حيث تبلغ القيمة الفعلية لمعامل التحويل 2.2046 باوند، وفيما يأتي بعض الأمثلة التي تُبين كيفية التحويل من كيلوغرام إلى باوند، ومن الباوند إلى كيلوغرام: مثال(1): كتلة وزنها 5.9 كيلوغرام، ما وزنها بالباوند؟ الحل: يُمكن حل هذا المثال

تعريف الخوارزمية سُمِّيت جداول الضرب والقسمة قديماً بالخوارزميات، وبعد أن تقدمت الحضارات واختُرِعت الحواسيب ارتبطت الخوارزميات بها ارتباطاً تاماً، وقد عُرِّفت بعدها الخوارزمية بأنّها مجموعة من الخطوات التي يستطيع الشخص الوصول عن طريقها إلى حلٍّ محدد؛ حيث تعالج الخوارزمية المعطيات والبيانات، وتجدر الإشارة هنا إلى أنّ هذه البيانات لا تقتصر على الأرقام والأعداد ، بل تفوق ذلك لتشمل الرسومات، والنصوص، والأصوات، والصور، وبصورة أخرى فإنّ الخوارزميّة هي قائمة من القواعد والتعليمات التي يجب اتباعها لحل

نظرة عامة حول تحليل مجموع مكعبين يمكن تعريف مجموع المكعبين (بالإنجليزية: Sum of Cubes) بأنه كثير حدود يكون على الصورة: أ³ ب³؛ حيث يكون على شكل حدين، تقصل بينهما إشارة جمع، وكل حد منهما مرفوع للقوة الثالثة، وتجدر الإشارة إلى أن الحدين هنا لهما نفس الإشارة بعكس الفرق بين مكعبين. لمزيد من المعلومات حول تحليل الفرق بين مكعبين يمكنك قراءة المقال الآتي: تحليل الفرق بين مكعبين . كيفية تحليل مجموع مكعبين يمكن تحليل مجموع المكعبين باستخدام الصيغة الآتية: س³ ص³= (س ص)( س²- س ص ص²)؛ حيث س هو الحد الأول،

طرق تحليل كثيرات الحدود يستخدم التحليل (بالإنجليزية: Factorization) لحل المعادلات الجبرية عادة، وهو يعني كتابة كثير الحدود على شكل حاصل ضرب كثيري حدود أو أكثر تقل درجتهما عن درجة كثير الحدود الأصلي، ويُطلق على كل كثير حدود ناتج من عملية التحليل اسم العامل، ولا يمكن تحليل أي عامل من هذه العوامل أبداً، كما يساوي حاصل ضرب جميع العوامل كثير الحدود الأصلي دائماً. لمزيد من المعلومات والأمثلة حول كثيرات الحدود يمكنك قراءة المقال الآتي: بحث عن كثيرات الحدود . أخذ العامل المشترك يتم التحليل من خلال هذه

التحليل العددي التحليل العددي (بالإنجليزية:Numerical analysis ) هو أحد فروع الرياضيات وعلم الحاسب الآلي (الكمبيوتر)، حيث يقوم على مبدأ إنشاء وتحليل وتنفيذ مجموعة من الخوارزميات للوصول إلى حلول رقمية للمشاكل الرياضية المبنية على التغيرات والتقلبات المستمرة، وقد تنشأ وتتكون هذه المشاكل والتحديات في العلوم الاجتماعية والطبيعية والطب والهندسة والأعمال، وقد يُطلَق على التحليل العددي مسميات أُخرى، مثل: الطرق العددية، أو التحليل الكمي. وقد أدى النمو الهائل للحواسيب الرقمية وتوفرها بكميات كبيرة إلى

تحليل المتجهات يُمكن إيجاد الإحداثي السيني (أس) والإحداثي الصادي (أص) للمتجه (أ) على النحو الآتي علماً بأنّ (أ) هي الوتر في المثلث القائم: أس= أ جتاθ. أص= أ جاθ. لإيجاد قيمة المتجه (أ) يتم استخدام قاعدة فيثاغورس كما يأتي: أ= (أس أص) ولإيجاد قيمة الزاوية التي ينحرف بها المتجه عن المحور السيني، يتمّ استخدام إحداثيات المتجه أس، وأص باستخدام خصائص المثلث، وذلك على النحو الآتي: ظاθ=∣أص÷أس∣. للحصول على الزاوية، نستخدم الاقتران العكسي للظل: θ=ظا∣أص÷أس∣ أمثلة على تحليل المتجهات سؤال: إذا كان مقدار

نظرة عامة حول الفرق بين مكعبين يعتبر الفرق بين مكعبين (بالإنجليزية: Difference of Two Cubes) حالة خاصة من كثيرات الحدود، والصيغة العامة له هي: س³- ص³، حيث إنّ: س³: هو الحَدِّ الأوّل ويجب أن يكون مكعباً كاملاً. ص³: هو الحَدِّ الثاني ويجب أن يكون مكعباً كاملاً. والإشارة بين الحدين هي إشارة فَرْقٍ أو طرح، وبهذا فهي تُمثِّل فَرقاً بين حَدَّين مكعبين، أو فَرقاً بين مكعبين. لمزيد من المعلومات حول تحليل الفرق بين مربعين يمكنك قراءة المقال الآتي: كيفية تحليل الفرق بين مربعين . كيفية تحليل الفرق بين

تحضير درس للرياضيات تعتبر مادة الرياضيات من المواد التي لا بُدّ من التحضير المسبق لها، ومحاولة إشراك الطلاب في العملية التدريسيّة التي تشتمل على الأرقام ومختلف العمليات الحسابيّة؛ كالجمع والضرب من خلال وضع الاستيراتيجات التي تساعد في ذلك داخل الغرفة الصفيّة، وتجدر الإشارة إلى ضرورة تهيئة الغرف الصفيّة لمادة الرياضيات ضمن بيئة تعليميّة جيدة؛ لتشجيع الطلاب على التفكير بطريقةٍ إيجابيّة والتمكن من طرح الدرس بسهولة، كما أن استخدام اساليب تدريس مختلفة للربط بين كلٍّ من المحتوى والمفاهيم والمهارات؛

علم الرياضيات علم الرياضيات: هو علم تحديد الكم وقياس الأشكال، كما يعد لغة العلوم النظرية والأدبية والفلسفية من خلال التحديد والضبط ليتم بناء محتوى العلم، وقد نشأ علم الرياضيات نظراً لحاجات الإنسان الضرورية، مثل الحاجة إلى تقسيم الطعام بين أفراد العائلة وتقسيم الأراضي وغنائم الحملات الحربية وقياس الوقت، كما يتم حساب كمية المحاصيل الزراعية وملاحة النجوم في السفر والترحال، وإجراء القياسات لتشييد الأبنية والمدن. نصائح لتحسين مهاراتك في الرياضيات قد يشعر البعض بأنهم سيئين بشكل طبيعي في الرياضيات،

تاريخ الرياضيّات منذ ما يقارب الثلاثة آلاف عام قام الكتبة البابليّون بممارسة كتابة حساب الفوائد والأعداد، وعلى وجه الخصوص في جميع أعمالهم التجاريّة في بابل، وكان يتمّ تدوين تلك العمليّات والأعداد على ألواحٍ صلصاليّة، مستخدمين قلم البوص المدبب في عمليّة التدوين تلك، ثم كانت توضع تلك الألواح في فرنٍ لتجف. كان قدماء البابليّين يعرفون العمليّات الحسابيّة كالجمع والطرح والضرب والقسمة، لكنهم لم يستخدموا في تلك العمليّات النظام العشري المستخدم في وقتنا الحاضر، وقد أدى هذا الأمر إلى زيادة تعقيدها

نظرة عامة حول الأعداد المركبة يمكن تعريف الأعداد المركبة (بالإنجليزية: Complex Number) بأنّها الأعداد التي تتكوّن من كل من الأعداد الحقيقية، والأعداد التخيلية (بالإنجليزية: Imaginary Number)، أما الأعداد التخيلية فهي تلك التي تُعطي نتيجة سالبة عند تربيعها، وهي بذلك تختلف عن الأعداد الحقيقية التي يساوي مربع أي عدد فيها قيمة موجبة؛ فتربيع أي عدد حقيقي موجب يُعطي نتيجة موجبة، كما أنّ تربيع أي عدد حقيقي سالب يُعطي نتيجة موجبة أيضاً؛ فمثلاً (-2) = 4؛ وذلك لأن -2×-2 = 4، وتضم جميع الأعداد التخيلية

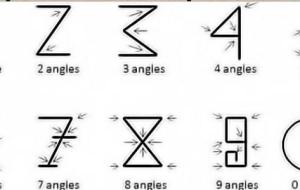
تعريف المثلث وخصائصه يُمكن تعريف المثلث (بالإنجليزية: Triangle) على أنه شكل مغلق ثنائي الأبعاد، وثلاثي الأضلاع، ويتكوّن من ثلاث قطع مستقيمة تُشكّل الأضلاع تتقاطع في نهايتها لتكوين الرؤوس أو الزوايا، وتتم تسمية المثلث غالباً بالاعتماد على رؤوسه، وله ثلاث زوايا يكون مجموع قياسها 180 درجة، ودائماً ما يقابل أقصر ضلع من المثلث أصغر زاوية داخلية، ويقابل أطول ضلع من المثلث أكبر زاوية داخلية، ومن أهمّ المصطلحات المتعلّقة بالمثلث ما يأتي: الرأس (بالإنجليزية: Vertex): هو زاوية المثلث، ويمتلك كلّ مثلث

الوسائل التعليميّة تعتبر الوسائل التعليميّة من أهمّ الطرق التي توصل المعلومات للتلاميذ بطرق بسيطة بعيدة عن التعقيد، وهي مهمةٌ في تدريس كلّ المواد التعليميّة وتزداد أهميتها في تدريس مادّة الرياضيات تحديداً؛ لأنّ مادّة الرياضيات تحتوي على مفاهيم في الهندسة والقياس والعمليات الحسابية المعقدة والجبر والبراهين وغيرها الكثير من المفاهيم، والتي يعاني الكثير من الطلاب من صعوبة فهمها وتعلّمها، لذلك لا بدّ من الإكثار من الوسائل التعليميّة المتنوّعة؛ لجعل مادّة الرياضيات أسهل وأكثر متعة في التعليم، ومن