قانون مساحة وحجم الكرة

قانون مساحة سطح الكرة

يُمكن تعريف مساحة سطح الكرة (بالإنجليزية: Surface area of a sphere) على أنه مقدار المساحة الإجمالية التي يشغلها سطح الكرة، ولإيجاد مساحة سطح الكرة يتم ضرب العدد (4) بالثابت باي، ثم ضرب الناتج بمربع نصف القطر، أي من خلال تطبيق المعادلة الآتية:

• مساحة سطح الكرة= 4×π×مربع نصف القطر، وبالرموز: م=4×π×نق²؛ حيث:
  • م: مساحة سطح الكرة.
  • نق: نصف قطر الكرة.
  • π: باي، ثابت عددي قيمته 3.14 أو 22/7.
• فمثلاً لحساب مساحة سطح الكرة التي تبلغ قيمة نصف قطرها 5سم يُمكن تطبيق القانون كما يأتي: تعويض قيمة نصف القطر نق في معادلة مساحة سطح الكرة= 4×π×نق²= 4×3.14×(5)²، لينتج أن مساحة سطح الكرة= 314سم².

تجدر الإشارة إلى أن قطر الكرة يساوي ضعفي نصف قطرها؛ أي أن: قطر الكرة=2 ×نصف قطر الكرة، وبالرموز: ق=2نق، أو نق=ق/2، وبالتالي يُمكن حساب مساحة سطح الكرة بتعويض قيمة القطر بدلاً من نصف القطر في القانون لينتج من ذلك أن مساحة سطح الكرة= 4×π×(ق/2)²، ثم بتبسيط المعادلة ينتج أن قانون مساحة سطح الكرة باستخدام القطر:

• مساحة سطح الكرة= مربع القطر×π ، وبالرموز:م=π×ق²؛ حيث:
  • م : مساحة سطح الكرة.
  • ق: قطرالكرة.
  • π: باي، ثابت عددي قيمته 3.14 أو 22/7.

كما يُمكن إعادة ترتيب المعادلة لحساب قيمة نصف القطر وذلك عند معرفة مساحة سطحها باستخدام المعادلة الآتية:

• نصف القطر=الجذر التربيعي للقيمة (مساحة سطح الكرة/4π)، وبالرموز: نق=(م/4π)√ ؛ حيث:
• م: مساحة سطح الكرة.
• π: باي، ثابت عددي قيمته 3.14 أو 22/7.
• نق: نصف قطر الكرة.

لمزيد من المعلومات والأمثلة حول مساحة الكرة يُمكنك قراءة المقال الآتي: قانون مساحة سطح الكرة .

قانون حجم الكرة

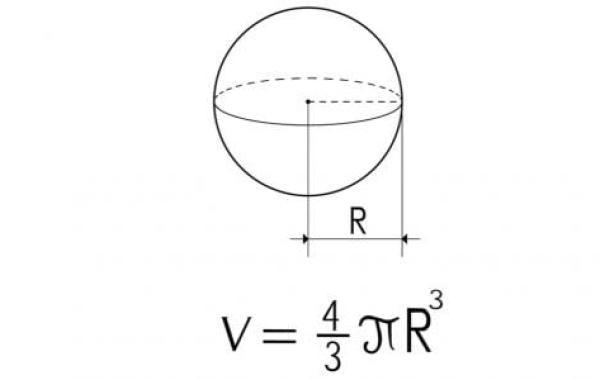
يُمكن تعريف حجم الكرة (بالإنجليزية: Sphere's Volume) على أنه كمية الفراغ الموجودة داخل الجسم ثلاثي الأبعاد، ويُقاس بالوحدات المكعّبة، ولإيجاد حجم الكرة يتم ضرب أربعة أثلاث الثابت العددي باي، بمكعب نصف القطر،لتنتج المعادلة الآتية:

• حجم الكرة=4/3×π×مكعب نصف القطر، وبالرموز: ح=4/3×π×نق³؛ حيث:
  • نق: نصف قطر الكرة.
  • π: باي، ثابت عددي قيمته 3.14 أو 22/7.
  • ح: حجم الكرة.
• ولإيجاد حجم الكرة التي نصف قطرها 3سم يُمكن تطبيق القانون كما يأتي: تعويض قيمة نصف القطر نق في معادلة حجم الكرة= 4/3×π×نق³= 4/3×3.14×(3)³، ومنه حجم الكرة= 113.04سم³.

لمزيد من المعلومات والأمثلة حول حجم الكرة يُمكنك قراءة المقال الآتي: قانون حجم الكرة في الرياضيات .

أمثلة على حساب مساحة وحجم الكرة

• المثال الأول: كرة نصف قطرها 6سم، ما هي مساحة سطحها، وما هو حجمها؟
  • الحل:
  • تعويض قيمة نصف القطر نق في معادلة مساحة سطح الكرة= 4×π×نق²= 4×3.14×(6)²، ومنه مساحة سطح الكرة= 452.16سم².
  • تعويض قيمة نصف القطر نق في معادلة حجم الكرة= 4/3×π×نق³= 4/3×3.14×(6)³، ومنه حجم الكرة= 904.32 سم³.

• المثال الثاني: نصف قطر مجسم مصغّر للكرة الأرضيّة هو 14سم، ما هي مساحة سطحها، وما هو حجمها؟
  • الحل:
  • تعويض قيمة نصف القطر نق في معادلة مساحة سطح الكرة= 4×π×نق²= 4×3.14×(14)²، ومنه مساحة سطح الكرة= 2461.76 سم².
  • تعويض قيمة نصف القطر نق في معادلة حجم الكرة= 4/3πنق³= 4/3×3.14×(14)³، ومنه حجم الكرة= 11,488.21سم³.

• المثال الثالث: تضاعف نصف قطر كرة إلى أربعة أضعاف نصف قطرها الأصلي، فإذا كان نصف قطرها الأصلي هو 4سم، فهل ستتضاعف مساحة سطحها أربع مرّات؟
  • الحل:
  • تعويض قيمة نصف القطر نق الأصلي في معادلة مساحة سطح الكرة= 4×π×نق²= 4×π×(4)²، ومنه مساحة سطح الكرة الأصلي= 64πسم².
  • تعويض قيمة نصف القطر نق المضاعف 4 مرات؛ أي الذي يساوي 4×4=16سم في معادلة مساحة سطح الكرة= 4×π×نق²=4×π×16²، ومنه مساحة سطح الكرة المضاعف 4 مرات = 1024πسم².
  • وبقسمة المساحة بعد مضاعفة نصف القطر على المساحة الأصلية ينتج أن: 1024πسم²/ 64πسم²= 16، ومنه فإن المساحة الأصلية قد تضاعفت 16 مرّة مقارنة بمساحة السطح الأصلي، ولم تتضاعف أربع مرّات.

• المثال الرابع: كرة قطرها 4م، ما هو حجمها؟
  • الحل:
  • حساب قيمة نصف القطر بقسمة القطر على 2 لينتج أن: نق= ق/2= 4/2= 2م.
  • تعويض قيمة نصف القطر نق في معادلة حجم الكرة= 4/3×π×نق³= 4/3×3.14×(2)³، ومنه حجم الكرة= 33.5م³.

• المثال الخامس: كرة حجمها 36π، ما هي مساحتها السطحيّة؟
  • الحل:
  • حساب قيمة نصف القطر نق بتعويض قيمة حجم الكرة في قانون حجم الكرة لينتج أن: π36= نق³×4/3×π، ومنه نق= 3سم.
  • تعويض قيمة نصف القطر نق في معادلة مساحة سطح الكرة= 4×π×نق²= 4×π×(3)²، ومنه مساحة سطح الكرة= 36πسم².

• المثال السادس: كرة مساحتها السطحية هي 100πسم²، ما هو نصف قطرها؟
  • الحل:
  • حساب قيمة نق بتعويض قيمة مساحة الكرة في قانون مساحة سطح الكرة لينتج أن: 100×π×4=π×نق² ، وبقسمة الطرفين على 4π، ينتج أن: 25= نق²، ومنه قيمة نق= 5سم.

• المثال السابع: كرة حجمها 14137.167سم³، ما هو نصف قطرها؟
  • الحل:
  • حساب قيمة نق بتعويض قيمة الحجم في قانون حجم الكرة= 4/3×π×نق³=14137.167، ومنه قيمة نق= 15سم.

• المثال الثامن: كرة شاطئ مساحتها السطحيّة 78.54سم²، ما هو نصف قطرها؟
  • الحل:
  • حساب قيمة نق بتعويض قيمة مساحة الكرة في قانون مساحة سطح الكرة، لينتج أن: 78.54= 4×π×نق² =4×3.14× نق²، ومنه قيمة نق= 2.5سم.

• المثال التاسع: ما هو حجم كرة الشاطئ السابقة؟
  • الحل:
  • تعويض قيمة نصف القطر نق في معادلة حجم الكرة= 4/3×π×نق³= 4/3×3.14×(2.5)³، ومنه حجم الكرة= 65.41 سم³.