قانون الجيب وقانون جيب التمام

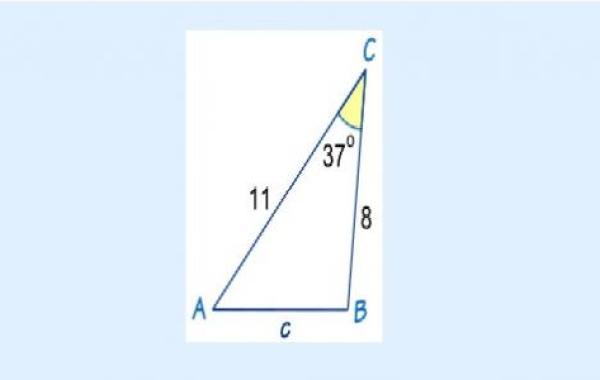
قانون الجيب

ينصّ قانون الجيب (بالإنجليزية: Sine Law) على أنه: "نسبة طول أي ضلع في أيّ مثلث إلى جيب الزاوية المُقابلة له هي قيمة ثابتة ومُتساوية بالنسبة لجميع أضلاع المُثلث"، وهذا ينطبق على كُلّ أنواع المُثلثات وليس فقط المُثلثات القائمة الزاوية، ويُستخدم قانون الجيب عندما يُعرف قياس زاويتين وضلع واحد، أو ضلعين وزاوية غير محصورة بينهما، لإيجاد أضلاع وزوايا المثلثات القائمة وغير قائمة الزاوية، وتكون صيغة القانون على صورتين على النحو الآتي:

• أ/جا(أَ) = ب/جا(بَ) = ج/جا(جَ) ، أو جا(أَ)/أ = جا(بَ)/ب = جا(جَ)/ج ، حيثُ تُمثّل أ، ب، ج أضلع المُثلث، بينما تُمثّل (أَ)، (بَ)، (جَ) الزوايا التي تُقابل كُل ضلع من الأضلاع.
• فمثلاً المثلث أ ب ج فيه الضلع أ ب=9 سم، وقياس الزاوية (أ ب ج)=76 درجة، وقياس الزاوية (أ ج ب)=58 درجة، ولإيجاد طول الضلع أج يُستخدم قانون الجيب على النحو الآتي:
  • 9/جا(58) = أج/جا(76)، وبضرب طرفيّ المُعادلة بـ جا(76) ينتج أنّ: أج=10.3 سم تقريباً.
  • لإيجاد طول الضلع ب ج أولاً يتمّ إيجاد قياس الزاوية (ج أ ب) التي تُقابله، حيثُ إن: الزاوية (ج أ ب) = 180- 58 – 76 = 46 درجة، ثمّ يُستخدم قانون الجيب على النحو الآتي: 9/جا(58) = ب ج/جا(46)، وبضرب طرفيّ المُعادلة بـ جا(46) ينتج أنّ: ب ج =7.63 تقريباً.

ولإثبات قانون الجيب يتمّ اتباع الخطوات الآتية:

• يُرسم مُثلث بحيثُ تكون أطوال أضلاعه أ، ب، ج، وزواياه التي تُقابل كل ضلع على الترتيب هي: الزاوية (أَ)، الزاوية (بَ)، الزاوية (جَ).
• إنزال خطّ عموديّ طوله ع على الضلع أ من الزاوية (أَ).
• التعويض في قانون جيب الزاوية على النحو الآتي: جا(بَ)=ع/ج، جا(جَ)=ع/ب، وبضرب الطرفين بـ (ج) في المعادلة الأولى لينتج أنّ: ع=ج×جا(بَ)، ثمّ ضرب الطرفين بـ (ب) في المُعادلة الثانية لينتج أنّ: ع = ب×جا(جَ).
• وبما أن كلتا المُعادلتين تساويان ع ينتج أنّ: ج×جا(بَ)=ب×جا(جَ).
• قسمة طرفيّ المُعادلة على جا(بَ)، ثمّ على جا(جَ)، لينتج أنّ: ج/جا(جَ)=ب/جا(بَ).
• تكرار الخطوات السابقة بإنزال خط عموديّ على الضلع ب من الزاوية (بَ) وتكرار الخطوات السابقة بالمثل، لينتج أنّ: ج/جا(جَ)=أ/جا(أَ).
• ثمّ بمساواة المُعادلات الناتجة من الخطوات السابقة ينتج أنّ: أ/جا(أَ)=ب/جا(بَ)= ج/جا(جَ).

لمزيد من المعلومات حول قانون الجيب يمكنك قراءة المقال الآتي: قانون الجيب في الرياضيات .

قانون جيب التمام

تكون الصيغة العامّة لقانون جيب التمام على النحو الآتي:

• ج²= أ² ب²-(2×أ×ب×جتا(جَ)).
• ب²= أ² ج²-(2×أ×ج×جتا(بَ)).
• أ²= ج² ب²-(2×ب×ج×جتا(أَ))؛ حيثُ إنّ:
  • أ، ب، ج ثمثّل أطوال أضلاع المُثلث، بينما تُمثّل (أَ)، (بَ)، (جَ) قياسات الزوايا التي تُقابل كُل ضلع من الأضلاع.

ملاحظة: إذا كان المُثلث قائم الزاوية في جَ فإن قيمة جتا(جَ)=جتا(90)=0، وبالتالي يُصبح القانون على النحو الآتي:

• ج²=أ² ب²، وهذه صيغة قانون فيثاغورس، مما يعني أنّ قانون الجتا هو قانون فيثاغورس مع وجود حدّ إضافي فيه.

يُستخدم قانون جيب التمام عندما يُعرف طول ضلعين وزاوية محصورة بينهما في المُثلث، أو عندما يُعرف طول الأضلاع الثلاث للمُثلث، ويُمكن أن يُكتب القانون على عدة أشكال لجعل الحلّ أسهل، فقد يكون القانون بدلالة جيب التمام للزوايا على النحو الآتي:

• جتا (أَ) = (ج² ب²-أ²)/ (2×ب×ج)
• جتا (بَ) = (أ² ج²-ب²)/ (2×أ×جـ)
• جتا (جَ) = (أ² ب²-ج²)/ (2×أ×ب)

• فمثلاً إذا كان المُثلث أب ج فيه الضلع أب=7 سم، والضلع أج=8 سم، والزاوية (ب أ ج)=110º، ولإيجاد قيمة الضلع ب ج، يتمّ التعويض في قانون جيب التمام: (ب ج)²=(7)² (8)²- (2×7×8×جتا(110º))، ومنه ينتج أنّ: (ب ج)²= 151.3، ثمّ بأخذ الجذر التربيعيّ للطرفين ينتج أنّ: ب ج=12.3 تقريباً.

ولإثبات قانون جيب التمام يتمّ اتباع الخطوات الآتية:

• يُرسم مُثلث بحيثُ تكون أطوال أضلاعه أ، ب، ج، وزواياه التي تُقابل كل ضلع على الترتيب هي: الزاوية (أَ)، الزاوية (بَ)، الزاوية (جَ).
• إنزال خطّ عموديّ طوله ع على الضلع ب من الزاوية (بَ)، وتُسمّى نقطة التقاء الخط مع الضلع ب بالنقطة د والتي تُقسّم الضلع ب إلى جزئين طولهما س و (ب-س).
• تطبيق نظريّة فيثاغورس على المثلث (أ ب د)، لينتج أنّ: ج²=ع² (ب-س)².
• تطبيق نظريّة فيثاغورس على المثلث (ب د ج)، لينتج أنّ: ع²=أ²- س².
• تعويض المُعادلة الثانية في المُعادلة الأولى، لينتج أنّ: ج²= (أ²- س²) (ب-س)²، ثمّ بفكّ الأقواس ينتج أنّ: ج²= أ²- س² ب²-2×ب×س س²، وبتبسيط المُعادلة ينتج أنّ: ج²=أ² ب²-(2×ب×س)، وبتعويض قيمة س= أ×جتا(ج) في المُعادلة ينتج أنّ: ج²=أ² ب²-(2×أ×ب×جتا(ج)).

لمزيد من المعلومات حول قانون جيب التمام يمكنك قراءة المقال الآتي: ما هو قانون جيب التمام .

أمثلة على قانون الجيب وقانون جيب التمام

• المثال الأول: المثلث أ ب جـ فيه طول الضلع أب=8 سم، أج=5 سم، ب ج=9 سم، جد قياس الزاوية (أ ج ب)؟
  • الحل:
  • تعويض أطوال أضلاع المُثلث في قانون جيب التمام؛ حيثُ يُعوّض طول أب مكان ج، ويُعوّض ب ج مكان أ، ويُعوّض أج مكان ب على النحو الآتي:
  • ج²= أ² ب² - (2 ×أ×ب×جتاجَ)، لينتج أنّ: (8)² =(9)² (5)²-(2×9×5×جتا(جَ))، ومنه: 64=81 25-(90×جتا(جَ))، ثمّ بتجميع الحدود ينتج أنّ: 64=106-(90×جتا(جَ))، ثمّ بطرح 106 من طرفيّ المُعادلة ينتج أنّ: -42=-90×جتا(ج)، ثمّ بقسمة الطرفين على العدد -90 ينتج أنّ: جتا(جَ)=42/90، ومنه: قياس الزاوية (جَ)=62.2 درجة.

• المثال الثاني: المثلث أ ب جـ فيه طول الضلع أج=6.5 سم، ب ج=9.4 سم، و قياس الزاوية (أ ج ب)=131 º، جد قياس الضلع أ ب؟
  • الحل:
  • تعويض أطوال أضلاع المُثلث في قانون جيب التمام؛ حيثُ يُعوّض طول أب مكان ج، ويُعوّض ب ج مكان أ، ويُعوّض أج مكان ب على النحو الآتي: ج²= أ² ب² - (2×أ×ب×جتاجَ)، لينتج أنّ:
  • (أب)² =(9.4)² (6.5)²-(2×9.4×6.5×جتا(131))، ومنه: (أب)² =88.36 42.25-(122.2×-0.656)، ثمّ بتجميع الحدود ينتج انّ: (أب)²=130.61-80.2 = 210.78، ثمّ بأخذ الجذر التربيعيّ للطرفين ينتج أنّ: أب = 14.5 سم تقريباً.

• المثال الثالث: المثلث أ ب جـ فيه طول الضلع أب= 9 سم، وقياس الزاوية (أ ب ج)=21 º، وقياس الزاوية (أ ج ب)=46 º، فأوجد الحلّ لهذا المُثلث (حلّ المُثلث: إيجاد أطوال أضلاعة وقياس زواياه)؟
  • الحل:
  • قياس الزاوية (ب أ ج)=180-(الزاوية (أ ب ج) الزاوية (أ ج ب))=180، ومنه: الزاوية (ب أ ج) = 180-(21 46) = 113 درجة.
  • لإيجاد طول الضلع أ ج يُستخدم قانون الجيب على النحو الآتي: ب/جا(بَ)=ج/جا(جَ)، لينتج: أج/جا(21) = 9/ جا(46)، وبضرب طرفيّ المُعادلة بـِ جا(21)، ينتج أنّ: أج= 4.5 سم.
  • لإيجاد طول الضلع ب ج يُستخدم قانون الجيب على النحو الآتي: أ/جا(أَ)=ج/جا(جَ)، لينتج: ب ج/جا(113)=9/جا(46)، وبضرب طرفيّ المُعادلة بـِ جا(113)، ينتج أنّ: ب ج= 11.5 سم.

• المثال الرابع: المثلث أ ب جـ فيه طول الضلع أب=5 سم، وقياس الزاوية (أ ب ج)=67 درجة، وقياس الزاوية (أ ج ب)=33 درجة، جد طول الضلع أ ج؟
  • الحل:
  • لإيجاد طول الضلع أ ج يُستخدم قانون الجيب على النحو الآتي: ب/جا(بَ)=ج/جا(جَ)، لينتج: أج/جا(67)=5/جا(33)، وبضرب طرفيّ المُعادلة بـِ جا(67)، ينتج أنّ: أج= 8.5 سم.

• المثال الخامس: المثلث أ ب جـ فيه طول الضلع ب ج=45 م، وقياس الزاوية (أ ب ج)=20 درجة، وقياس الزاوية (ب أ ج)=30 درجة، جد الحلّ لهذا المُثلث (حلّ المُثلث: إيجاد أطوال أضلاعه وقياس زواياه)؟
  • الحل:
  • قياس الزاوية (أ ج ب)=180-(الزاوية (أ ب ج) الزاوية (ب أ ج))=180-(20 30) = 130 درجة.
  • لإيجاد طول الضلع أ ج يُستخدم قانون الجيب على النحو الآتي: ب/جا(ب)=أ/جا(أ)، لينتج أن: أج/جا(20)=45/جا(30)، وبضرب طرفيّ المُعادلة بـِ جا(20)، ينتج أنّ: أج=30.8 م.
  • لإيجاد طول الضلع أب يُستخدم قانون الجيب على النحو الآتي: ج/جا(جَ)=أ/جا(أَ)، لينتج: أب/جا(130)= 45/جا(30)، وبضرب طرفيّ المُعادلة بـِ جا(130)، ينتج أنّ: أب=68.9 م.

• المثال السادس: المثلث أ ب جـ فيه طول الضلع أب=8 سم، أج=5 سم، ب ج=7 سم، جد قياس الزاوية (ب أ ج)؟
  • الحل:
  • تعويض أطوال أضلاع المُثلث في قانون جيب التمام؛ حيثُ يُعوّض طول أب مكان ج، ويُعوّض ب ج مكان أ، ويُعوّض أج مكان ب على النحو الآتي: أ²= ب² ج² -(2×ب×ج×جتا أَ)، لينتج أنّ: (7)² =(5)² (8)²-(2×5×8×جتا(أَ))، ومنه: 49=25 64-(80×جتا(أَ))، ثمّ بتجميع الحدود ينتج انّ: 49=89-(80×جتا(أ))، ثمّ بطرح 89 من طرفيّ المُعادلة ينتج أنّ: -40=-80×جتا(أَ)، ثمّ بقسمة الرقمين على الرقم -80 ينتج أنّ: جتا(ج)=-0.5، ومنه: الزاوية(أ)=60 درجة.

• المثال السابع: طول الضلع ب=10 سم، ج=3 سم، وقياس الزاوية (جَ)=45 درجة، فجد الحلّ لهذا المُثلث إن أمكن؟
  • الحل:
  • تعويض القيم في قانون الجيب: ج/جا(جَ)=ب/جا(بَ)، لينتج أنّ: جا(45)/3=جا(بَ)/10، وبضرب طرفيّ المُعادلة في 10، ينتج أنّ: جا(بَ)=جا(45)/30=2.36، وبما أنّ أكبر قيمة للجيب تساوي 1، وهذا مستحيل من ناحية رياضيّة، فبالتالي المعلومات المُعطاة لا تُشكل مُثلثاً.

• المثال الثامن: محطة رصد واقعة على النقطة (و)، وتبعد عنها الطائرة (ع) مسافة 50 كم، وتبعد عنها الطائرة (ل) مسافة 72 كم، فيتشكّل المُثلث و ع ل، فإذا كان قياس الزاوية (ع و ل)=49 درجة، فجد المسافة بين الطائرتين في تلك اللحظة والتي تُمثّل الضلع ع ل؟
  • الحل:
  • بافتراض أن الضلع (ع ل)=أ، وع=ب، ول=ج، يتمّ تعويض القيم في قانون جيب التمام:
  • أ²= ب² ج² -(2×ب×ج×جتا أَ)، ومنه: (ع ل)²= ²50 72²-(2×50×72×جتا 49)=2500 5184-7200×0.656=2959.4، وبأخذ الجذر التربيعيّ للطرفين ينتج أنّ: (ع ل)=54.4 كم.

• المثال التاسع: سفينة غادرت النقطة (أ) في الميناء باتجاه الشمال عند الساعة الواحدة مساءً بسرعة 30 كم/ساعة، ثمّ عند الساعة الثالثة مساءً غيّرت اتجاه حركتها عند النقطة (ب) بمقدار 20 درجة باتجاه الشرق، جد بعد هذه السفينة عن النقطة (أ) عند وصولها إلى النقطة (ج) عند الساعة الرابعة مساءً؟
  • الحل:
  • المدة الزمنيّة التي استغرقتها السفينة للوصول من النقطة (أ) إلى النقطة (ب)=3-1=2 ساعة، كما أنّ المدة الزمنيّة التي استغرقتها السفينة للوصول من النقطة (ب) إلى النقطة (ج)=4-3=1 ساعة.
  • حركة السفن تشكّل مثلثاً هو المثلث (أ ب ج)، يُمكن حساب طول الضلع أ ب فيه عن طريق ضرب السرعة في المدة الزمنية التي استغرقتها السفينة للوصول من النقطة (أ) إلى النقطة (ب): أب= السرعة× الزمن=30×2=60 كم، وهو الأمر نفسه بالنسبة للضلع (ب ج)=30×1=30 كم.
  • قياس الزاوية (أ ب ج) =180-20=160 درجة؛ لأن السفينة غيّرت اتجاهها بمقدار 20 درجة نحو الشرق من الشمال.
  • حساب بُعد السفينة عن النقطة (أ) عن طريق تعويض (أج) مكان ب، (أب) مكان ج، (ب ج) مكان أ في قانون جيب التمام: ب²= أ² ج² - (2×أ×ج×جتا بَ)، لينتج أنّ: (أج)²= ²30 ²60-(2×30×60×جتا160)=900 3600-(3600×-0.94)=7882.9، وبأخذ الجذر التربيعيّ للطرفين ينتج أنّ: أج=88.8 كم.

لمزيد من المعلومات حول قوانين حساب المثلثات يمكنك قراءة المقال الآتي: قوانين حساب المثلثات .