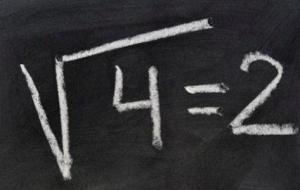تعليم

أنواع النعت الحقيقي ينقسم النعت الحقيقي باعتبار لفظه إلى ثلاثة أقسام، وهي كالآتي: النعت المفرد وهو ما ليس جملة ولا شبه جملة، مثل: (القاهرة مدينةٌ عظيمةٌ)، فكلمة "عظيمة" تُعرب: (نعت لِـ "مدينة" مرفوع وعلامة رفعه تنوين الضم الظاهر على آخره)، ورفع النعت هنا لأنَّه تابع للمنعوت في حكمه الإعرابي، وبما أنَّ كلمة "مدينة" مرفوعة لأنَّها خبر المبتدأ، يكون نعتها مرفوعاً أيضاً. النعت الجملة ويُشترط في المنعوت بالجملة أن يكون نكرة، وأنْ تكون الجملة مشتملة على ضمير يربطها بالمنعوت، وهذه الجملة نوعان هما

مفهوم المعرفة المعرفة هي الاسم الذي وُضع ليستعمل في الدلالة على شيءٍ معين ومعلوم وهي ستة أقسام: الضمير مثل (أنا وأنت)، والعلم مثل (محمد وفاطمة)، واسم الإشارة مثل (هذا وهذه)، والاسم الموصل مثل (الذي والتي)، والمعرف بأل مثل (القلم والحقيبة) والمضاف لمعرفة مثل (حقيبة محمد وكتاب النحو)، والضمير هو أقوى المعارف يليه العلم ثم اسم الإشارة ثم الاسم الموصول ثم المعرف بأل، وهكذا حتى يكون المضاف إلى معرفة أقلها تعريفًا ودلالة على شيءٍ معين. أنواع المعرفة الاسم المعرف ثلاثة أقسام: أولها: صيغة معينة وجدت

النسبة يتمّ تعريف النّسبة (Ratio) رياضيًا على أنّها العلاقة بين مجموعتين حسابيًا أو رياضيًا، بحيث تعبّر هذه العلاقة عن مدى مجموعةٍ أكبر من مدى المجموعة الأخرى، ويتمّ المقارنة بين هاتين المجموعتين عن طريق قسمة أحدهما على الأخرى لحساب النّسبة بينهما، ولحساب النّسبة بين مجموعتين عدديتين فإنّ العلاقة بينهما تكون كما يأتي: نسبة المجموعة (أ) إلى المجموعة (ب) = قيمة المجموعة (أ) / قيمة المجموعة (ب) وإذا أردنا حساب النسبة المئوية فإننا نقوم بضرب النسبة 100x% فيصبح القانون: قيمة المجموعة (أ) / قيمة

تعريف الميزان الصرفي إنّ الميزان الصّرفي هو معيارٌ لفظي يُعرف من خلاله ما يُزاد على أحرف الكلمة الأصليّة ، وكذلك ما يطرأ من تغييراتٍ على الكلمة، فالميزان الصّرفي شأنه شأن أيّ ميزانٍ في الحياة يُعرف به مقادير الأشياء، وهذا الميزان يُعرف به مقادير الكلمات وأوزانها، فقد وضعه علماء اللغة العربية متّخذين كلمة "فعل" طريقًا لوزن الكلمات. شرح الميزان الصرفي في اللغة العربية يمكن شرح الميزان الصرفي من خلال الإضاءة على عدة نقاط، هي: وزن الكلمات المجردة إنّ الأصول المجرّدة للكلمات في اللّغة العربيّة ،

المنصوبات من الأسماء الاسم المنصوب إمَّا أن يكون عمدة كالمفاعيل الخمسة ، واسم إنَّ وخبر كان أو فضلة كالتمييز أو الحال، ومن جهة أخرى قد يكون متبوعاً له حكمه الخاص، أو تابعاً يأخذ حكم متبوعه، وبالتالي المنصوبات الخمسة عشر تشمل أربعة أقسام رئيسة، نذكر أهمها في المقال. المفاعيل المفعول المطلق وهو المصدر، وسُمي مطلقاً لعدم تعلقه بأداة كما هو الحال في باقي المفاعيل، ويأتي ثالثاً في تصريف الفعل نحو: صام يصوم صوماً؛ صوماً: مفعول مطل ق منصوب وعلامة نصبه الفتحة الظاهرة. المفعول به وهو ما وقع عليه الفعل

تعريف المفعول المُطلَق المفعول المُطْلَق؛ هو مصدر منصوب يدل على مُطلق حدوث الفعل، ويأتي مؤكدًا على فعله أو مبينًا لنوعه أو عدده، وجدير بالذكر أنّ المفعول المُطلَق سُمّيَ بهذا الاسم؛ لعدم تقيُّده بحرف جرّ أو غيره من المُقيِّدات كالمفاعيل الأخرى مثل: المفعول فيه، و المفعول به ، والمفعول له، والمفعول معه، فكُلُّها مفاعيل مُقيّدة بحرف جرّ، ولهذا أصبح المفعول المطلق مُطلقًا أيّ أنّه حر وغير مُقيّد. التعريف عند علماء اللغة تعددت تعريفات المفعول المطلق عند عُلماء الّلغة العربية، فابن مالك وأبو حيّان

شرح المفرد والمثنى والجمع يُقسم الكلام في اللغة العربية من حيث الإفراد والتثنية والجمع أي العدد إلى ثلاثة أقسام على النحو الآتي: الاسم المفرد هو كل اسم دلّ على شيء واحد مذكرًا كان أم مؤنثًا، مثل: (حقيبة) (قلم) (مرآة) (طائر)، والاسم المفرد إذا جاء في الجملة فإنه يعرب حسب موقعه وتظهر عليه علامات الإعراب الثلاثة: (الفتحة والضمة والكسرة)، مثل ما يأتي: قرأ معاذُ قصةً. عالجَ الطبيبُ أميرةَ. إنّ الاسم (قصة) هو اسم مفرد مؤنث وموقعه الإعرابي في الجملة جاء (مفعولًا به)، وعند الإعراب نقول: مفعول به منصوب

شرح المعادلات الخطية المعادلة الخطية هي معادلة جبرية حيث يكون الحد الرئيسي مرفوعًا للقوة 1، وعندما يتم رسم هذه المعادلة فإنها تؤدي دائمًا إلى خط مستقيم وهذا هو سبب تسميتها بـ "المعادلة الخطية". بمعنى آخر يعني ذلك أن المعادلة التي تحتوي على أعلى درجة أسية ذات القوة 1 فإنها تعرف باسم المعادلة الخطية، هذا يعني أنه لا يوجد متغير في المعادلة الخطية له أس أكبر من 1 حيث يشكل الرسم البياني للمعادلة الخطية عند رسمه دائمًا خطًا مستقيمًا. المعادلات الخطية تكون بمتغير واحد أو اثنين أو ثلاثة كما يأتي:

شرح المضلعات المتشابهة تُعرّف المضلعات المتشابهة (بالإنجليزية: Similar Polygons) بأنّها المضلعات الهندسية التي تتشابه في الشكل الخارجي ولكنها تختلف في الحجم، وبالتالي فإنّها تشترك فقط في قياس الزوايا المتناظرة وتتناسب في أطوال الأضلاع المتناظرة. بينما تُعرّف المضلعات (بالإنجليزية: Polygons) بأنّها أشكال هندسية ثنائية الأبعاد تتكون من خطوط مستقيمة، ومن الأمثلة عليها: المستطيل، والمربع، والنجوم، والمثلث، وبالتالي لا يُمكن تسمية الدائرة مضلع لأنّه تتكون من خطوط منحنية. على سبيل المثال: إذا كان

تعريف المضاف والمضاف إليه تركيب الإضافة هو ما تكوّن من كلمتين أولاهما تسمى (مضافًا)، وثانيهما تسمّى (مضافًا إليه)، فهو نسبةٌ بين اسمين على تقدير حرف جرّ بينهما. ويكون تركيب الإضافة في الجملة الاسميّة و الجملة الفعليّة على حد سواء، كما يمكن تمييز هذا التركيب ومعرفة المضاف والمضاف إليه من خلال المعنى، فكلا الاسمين متعلقان ببعضهما من حيث المعنى لا يمكن قطع أحدهما على الآخر، وكأنّ هناك رابطٌ بينهما خفيّ لا يبرز، لذا لا يجوز دخول شيء بين المضاف والمضاف إليه حتى لا ينفكّ هذا المعنى عنهما. كيفية

تعريف الفعل المضارع تقسم الأفعال حسب زمن حدوثها إلى ثلاثة أقسام، وهي الفعل الماضي والفعل المضارع وفعل الأمر، ويمكن تعريف الفعل المُضارع على أنه لفظ يدل على حصول عمل في الزمن الحاضر أَو المُسْتَقبَلِ، وذلك كما في جملة (يلعبُ أحمدُ بالكرة) فإنّ الفعل (يلعب) يَدُلّ عَلَى حصول اللّعب في الزمن الحاضر أو المستقبل، وكذلك في جملة (أغسلُ يديّ) فإنّ الفعل (أغسل) دُلّ عَلَى حصول الْغَسْل في الزمن الحاضر أو المستقبل. طريقة صياغة الفعل المضارع يُصاغ الفعل المضارع من الفعل الماضي من خلال زيادة أحد أحرف

المصدر النائب عن فعله المصدر النائب عن فعله هو مصدر ينوب عن فعله ويؤدي معناه، ولا يجوز أن يجتمع مع فعله ما دام ينوب عنه ويؤدي ما يؤديه، ويختلف المصدر النائب عن فعله عن المفعول المطلق بأنه يكون طلبيًا أو مشبهًا بالطلبي، إضافة إلى أنه يعمل عمل فعله فاعلًا و مفعولًا به . المصدر الذي يقع موقع الأمر أو النهي ومن الأمثلة عليه ما يأتي: انتقامًا من المجرمين. حزنًا على الفقراء والمساكين. فرحًا بنتائج الثانوية العامة. خجلًا من الرجال أصدقاء أبي. فالمصادر التي تحتها خط في الأمثلة السابقة هي مصادر نابت عن

شرح المشبه والمشبه به للأطفال نحن نعرف أن التشبيه في اللغة العربية يعج من الأساليب اللغوية وهو يعني اشتراك شيئين أو أكثر في صفة أو أكثر بأداة، فعندما نقول الفتاة كالقمر نعني بذلك أن الفتاة تشبه القمر لأنها جميلة، ولو قلنا الطلبة المجتهدون كالنجوم اللامعة في السماء نعني أن الطلبة يشبهون النجوم اللامعة لأنهم متميزون. كيف نستخرج التشبيه من الجمل؟ وفيما يأتي أمثلة مع الشرح الموضح على التشبيه: الفتاةُ متألقةٌ كالبدرِ في السماء المظلمة. البستانُ جميلٌ وخلّاب كالجنّة. سامي سريعٌ مثل الحصانِ. ختام

شرح المربعات الكاملة في الرياضيات المربعات الكاملة (بالإنجليزية: Perfect Squares) هي الأعداد الناتجة عن حاصل ضرب عدد صحيح في نفسه، على سبيل المثال، حاصل ضرب الرقم 2 في نفسه هو عبارة عن 2 × 2 ويساوي 4، أي أن الـ 4 مربع كامل. رمز المربع الكامل يُرمز إلى مربع العدد بالرمز أس 2، أو تربيع، أو ^2، ودائماً ما يكون المربع الكامل موجباً، ولا يمكن أن يكون سالباً، حتى لو كان ناتجاً عن ضرب عدد سالب بنفسه: س × س = س ² ، و - س × - س = س ² . مثال: 5 × 5 = 5 ² = 25، وأيضاً - 5 × - 5 = (- 5) ² = 25 طرق تحديد

شرح المدى والوسيط والمنوال في الرياضيات يُستخدم المدى، والوسيط، والمنوال في التوزيعات الإحصائية لقيم معينة، حيث تساعد هذه الخصائص في تحليل البيانات ، وتلخيصها، للوصل إلى استنتاج معين، وفيما يلي شرح تعريف وطريقة حساب المدى، والوسيط، والمنوال في الرياضيات : الوسيط Median يمكن حساب الوسيط عن طريق إيجاد القيمة، أو الرقم الذي بالوسط، ولكن يجب ترتيب القيم من الأصغر إلى الأكبر أولاً، كما يجب معرفة عدد القيم، فإذا كان العدد زوجياً، فهذا يعني أنه يوجد رقمان في الوسط، وفي هذه الحالة، يجب إيجاد المتوسط

المدرسة الكلاسيكية في العمارة العمارة الكلاسيكية؛ نوع من المباني التي بناها الإغريق والرومان الأوائل، تحديدًا بين القرنين الخامس قبل الميلاد (في اليونان) والقرن الثالث الميلادي (في روما)، ومنذ ذلك الوقت استعمل المعماريون العمارة الكلاسيكية أساسًا لأعمالهم كلّما أرادوا الحصول على الإلهام، أو عندما يُريدون ابتكار شيء جديد. إنّ العمارة خلال عصر النهضة مثال واضح على العمارة الكلاسيكية، بالإضافة إلى العمارة في النهضة اليونانية في القرن التاسع عشر، وفي بريطانيا الفيكتورية وغيرها من أوروبا، حاول

شرح المثنى المذكر والمثنى المؤنث كان الأصل قديمًا في كل اسم نريد صياغة صيغة تدل على المثنى منه أن نأتي به معطوفًا مثل: جاء العامل، فلو أردنا صياغة صيغة تدل على المثنى منها كنا نقول: جاء العاملُ والعاملُ أو مررتُ بالعاملِ والعاملِ أو أحضر أبي العاملَ والعاملَ، بالعطف على المثيل ولكن الإيجاز في لسان العرب دعا إلى إلحاق زيادة بالكلمة المراد تثنيتها تغني عن العطف بالمثيل لتجنب التطويل والتكرار. المثنى المذكر وهو كل اسم دلّ على اثنين بزيادة ألف ونون في حالة الرفع أو ياء ونون في حالتي النصب والجر،

المبني من الأسماء تقسم الأسماء في اللغة العربية إلى أسماء معربة وأسماء مبنية، الأسماء المبنية هي التي تلزم حركة واحدة دون تغيير، وتكون مبنية على الضم أو الفتح أو الكسر أو السكون، وتشمل: أسماء الإشارة، والأسماء الموصولة، و أسماء الاستفهام ، والضمائر، وبعض الظروف، والأعداد (11-1)، وسيتم توضيحها فيما يأتي: أسماء الإشارة أسماء تستخدم للإشارة إلى الأشياء، وهي: هذا، هذه، هذي، ها، هنا، ذاك، تلك، ذلك، هنا، هنالك، هؤلاء، أولئك، وجميعها مبنية، أما اسما الإشارة (هذان، هاتان) فهما معربان وملحقان بالمثنى،

شرح المبتدأ والخبر للأطفال يقسم الكلام في اللغة إلى أسماء وأفعال وحروف، وجميعها معًا تكوّن جُملًا، والجمل في اللغة أنواع ومنها الجمل الاسمية والجمل الفعلية وكل جملة تتكون من أركان، فالجملة الاسمية تتكون من ركنين أساسيين هما: المبتدأ والخبر، والجملة الفعلية تتكون من ركنيين أساسيين هما: الفعل والفاعل أو الفعل ونائب الفاعل، ويعد المفعول به وغيره أركانًا ثانويةً في الجمل الفعلية. ما هو المبتدأ؟ المبتدأ كما ذكرنا سابقًا هو أحد أركان الجملة الاسمية، ويُعرف بأنه كل كلمة جاءت في بداية الكلام ويكونُ

شرح المادة الغازية للأطفال المادة الغازية أو الغاز هو حالة من حالات المادة الثلاثة بجانب الصلب والسائل، وأكثر ما يُميز الغازات عن غيرها من المواد أنها ليس لها حجم محدد أو شكل محدد على عكس المادة الصلبة التي لها شكل ثابت، والمادة السائلة التي لها حجم محدد، ولكن على الرغم من ذلك تستهلك المادة الغازية حيزًا ولها كتلة كغيرها من المواد،وإليك الخطوات التالية لشرح المادة الغازية للأطفال: تعريف المادة الغازية قد يكون شرح المادة الغازية للأطفال أمرًا صعبًا قليلًا، وذلك لأنها غير مرئية، ولكن باستطاعتك

مفهوم اللسانيات التطبيقية تعتبر اللسانيات التطبيقية علم حديث أتى نتاج مجموعة من العلوم المختلفة، وهو تطبيق لمعطيات السانيات النظرية التي تتصدى لحل مشكلاتها بأن يرفد الأسس المعرفية لها ليحقق حالة من التوازن بين النظرية والتطبيق. تعرَف اللسانيات التطبيقية بأنها نقطة التقاء العديد من علوم الإنسان ؛ أي أنها تتناول الإنسان في جوهره كإنسان ناطق، وتبين المشكلات النوعية له، وتسعى لتحديد المشكلات التي تعيق ذلك، والضوابط المحددة لهذا الأمر. علم اللغة التطبيقي أحد مجالات الدراسة التي تشرح كيفية مساعدة

كيفية شرح الكسور المتساوية الكسر في الرياضيات يتضمن البسط وهو الرقم الموجود أعلى إشارة القسمة، ويتضمن المقام وهو الرقم الموجود أسفل إشارة القسمة، مثل: (1/2)، حيث يمثل الرقم 1 البسط، بينما يمثل الرقم 2 المقام لهذا الكسر، أمَّا الكسور المتساوية هي عملية تكوين نفس قيمة الكسر الموجود باستخدام عمليتي الضرب والقسمة، لذا يمكن إيجاد عدد كبير من الكسور المساوية لنفس قيمة الكسر المطلوب. تعريف الكسور المتساوية بالرسم من الطرق الممتعة لتعليم الأطفال مفهوم الكسور، والكسور المتساوية هي الرسم باستخدام

تعريف القياس غير المباشر يعرف القياس غير المباشر على أنه الأسلوب الذي يتم من خلاله جمع المعلومات والبيانات بطريقة كمية وباستخدام أدوات خاصة لقياس الأشياء التي يصعب استخدام القياس المباشر لإيجادها، ويتم ذلك من خلال حساب مجموعة البيانات التي تم جمعها من واحد أو أكثر من الكميات المادية المختلفة، ولا يتم الحصول عليه من خلال أداة معينة، ومن أمثلة ذلك تحديد الوقت بالنظر إلى الساعة. ما الفرق بين القياس المباشر وغير المباشر؟ هناك فروقات عدة بين القياس المباشر وغير المباشر، أهمها: أن القياس المباشر يتم

القانون الأول في الديناميكا الحرارية ينص القانون الأول في الديناميكا الحرارية على أن الحرارة هي شكل من أشكال الطاقة ، وبالتالي تخضع لقانون حفظ الطاقة الذي ينص على أن الطاقة لا تفنى ولا تخلق من العدم وإنما تتحول من شكل إلى آخر، أي أن الطاقة الكلية للنظام تظل ثابتة، ويُعتبر القانون الأول في الديناميكا الحرارية امتداد لقانون حفظ الطاقة، وهناك أمثلة عديدة في حياتنا اليومية توضح هذه الظاهرة، فمثلًا الطاقة الحركية في السيارة (الطاقة الحركية: هي الطاقة التي يمتلكها الجسم عندما يتحرك)، تتحول إلى طاقة