تعليم

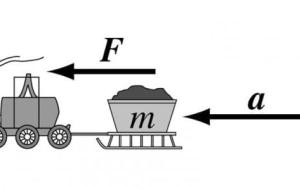
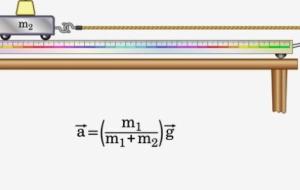
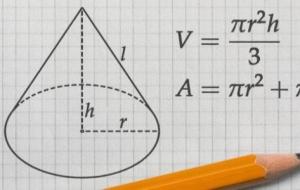نص قانون نيوتن الثاني يحاكي قانون نيوتن الثاني (بالإنجليزية: Newton's Second Law) حركة الجسم وسلوكه في حال تأثره بقوى غير متوازنة، حيث ينص على " أنّ تسارع أي جسم ناتج عن قوة مؤثرة عليه، يتناسب تناسباً عكسياً مع كتلة الجسم، وطردياً مع مقدار القوة وفي نفس اتجاهها "، ويعد قانون نيوتن الثاني أحد قوانين نيوتن في الحركة . الصيغة الرياضية لقانون نيوتن الثاني يُعبر عن قانون نيوتن الثاني بالصيغة الرياضية الآتية: القوة المؤثرة في الجسم= كتلة الجسم × تسارع الجسم بالرموز: ق = ك × ت بالإنجليزية: F = m × a

نص قانون نيوتن الثالث ينص قانون نيوتن الثالث للحركة على أنّ: (لكلّ فعل رد فعل مساوٍ له في المقدار ومعاكس له في الاتجاه)؛ حيث يعبّر هذا القانون عن ردة الفعل الناتجة عند التأثير بقوّة من جسمٍ ما على جسمٍ آخر، أي أنه عند التأثير بقوّة معينة في جسمٍ ما فإنّ ذلك الجسم سيؤثّر فيه بقوّة بالمقابل تعادل القوّة المبذولة عليه وتعاكسها قي الاتجاه، وفيما يأتي بعض الأمثلة على هذا القانون: تدفع الأرض جسم الإنسان للأعلى، عندما تسحبه قوّة الجاذبيّة الأرضيّة إلى الأسفل. تدفع عربة التسوق السائث باتّجاه معاكسٍ

نص قانون نيوتن الأول ينصّ قانون نيوتن الأول (بالإنجليزية: Newton's first law) على أنّ الجسم الساكن يبقى ساكنًا، والجسم المتحرك يبقى متحركًا بسرعة ثابتة وفي نفس الاتجاه، ما لم تُؤثّر فيه قوة خارجية تُغيّر من حالته، وهو ما يُعرف أيضاً بقانون القصور الذاتي (بالإنجليزية:Inertia)،و الذي يعتمد على كتلة الجسم، فكلّما كانت الكتلة أكبر كان تحريك أو تغيير اتجاه وسرعة الجسم أكبر وأصعب. أمثلة على قانون نيوتن الأول هناك العديد من الأمثلة المتعلقة بقانون نيوتن الأول، ومنها ما يأتي: إطلاق صاروخ عبر الغلاف

نص قانون نيوتن الأول ينص قانون نيوتن الأول على أن: الجسم الساكن يبقى ساكناً والجسم المتحرك في خط مستقيم وسرعة محددة يبقى كذلك ما لم تؤثر عليه قوة خارجية تدفعه أو تسحبه. بعبارةٍ أخرى الجسم سيحافظ على حالته الحركية إذا كانت القوة الخارجية صفراً ، لكن إذا أثرت عليه قوة خارجية فإنّ حالته الحركية ستتغير من السكون إلى الحركة، بمعنى أنّه لا يمكن للجسم تغيير حركته أو سرعته من تلقاء نفسه، مع الأخذ بعين الاعتبار اختلاف سرعة الجسم باختلاف القوة الخارجية . تطبيقات على قانون نيوتن الأول كثيرةٌ هي التطبيقات

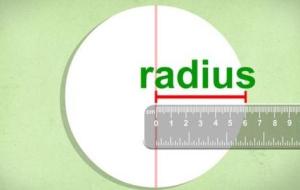
كيفية حساب نصف قطر الدائرة يُعرّف نصف القطر الدائرة (بالإنجليزيّة: Radius of Circle) بأنّه الخط المستقيم الواصل بين مركز الدائرة ونقطة تقع على محيطها، ويُمكن حسابه بعدّة طرق وفقًا للمعطيات المتوفرة، وهي كالآتي: حساب نصف القطر من محيط الدائرة يُمكن حساب نصف القطر للدائرة عندما يكون محيطها معلومًا عن طريق الآتي: كتابة قانون محيط الدائرة : محيط الدائرة = 2 × π × نصف القطر إعادة ترتيب قانون المحيط وجعل نصف القطر موضوع القانون ينتج الآتي: نصف القطر = المحيط / 2 × π وبالرموز: نق = ح / 2 × π حيث إنّ:

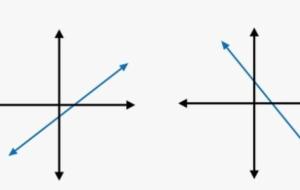
قوانين حساب ميل المستقيم يمكن حساب ميل المستقيم عن طريق إحدى الطرق الآتية: ميل المستقيم باستخدام النقاط للخط المستقيم الميل ذاته في كل مكان؛ لذلك يمكن تحديد ميله من خلال استخدام أي نقطتين واقعتين عليه، وذلك باتباع الخطوات الآتية: تحديد نقطتين على الخط المستقيم. اختيار إحداهما لتمثل (س 1، ص 1)، والأخرى لتكون (س 2، ص 2). حساب الميل باستخدام قانون حساب ميل المستقيم عن طريق تعويض قيم النقطتين السابقتين فيه، وهو: ميل المستقيم = الفرق في الصادات/الفرق في السينات وبالرموز؛ (م)= (ص 2- ص 1) / (س2-س1)

ما هو قانون مور؟ يقصد بقانون مور (بالإنجليزية: Moore's law) التنبؤ الذي وضعه المهندس الأمريكيّ جوردن مور حول قطعة إلكترونيّة تُدعى الترانزستور، وينصّ القانون على أنّ عدد الترانزستورات (بالإنجليزية: Transistors) لكل رقاقة سيليكون يتضاعف كلّ عام. ويقصد بالترانزستورات قطع إلكترونيّة مصنوعة من أشباه الموصلات، و يساعد الترانزستور في توليد الإشارات الكهربائية وتضخيمها ، والتحكم بها. وضع المهندس مور هذا التبنؤ عام 1965م، واستمر مور بالملاحظة المضاعفة التي تحدث للترانزستورات، لكن النتيجة كانت أبطأ من

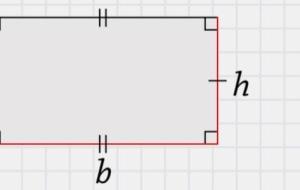
قوانين مساحة المستطيل يمكن حساب مساحة المستطيل باستخدام قوانين عدة وفق حالات محددة، وذلك كما يأتي: قانون مساحة المستطيل عند معرفة الطول والعرض يمكن حساب مساحة المستطيل باستخدام القانون البسيط الآتي: مساحة المستطيل=الطول×العرض، وبالرموز: م=أ×ب حيث: م: مساحة المستطيل. أ: طول المستطيل. ب: عرض المستطيل. قانون مساحة المستطيل عند معرفة القطر وأحد الأبعاد يمكن حساب مساحة المستطيل باستخدام القانون الآتي: مساحة المستطيل= الطول أو العرض×الجذر التربيعي لـ (مربّع القطر- مربع الطول أو مربع العرض) ،

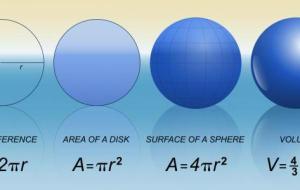
قانون مساحة الدائرة يُمكن تعريف مساحة الدائرة (بالإنجليزية: Area of a Circle) بأنّها المساحة أو المنطقة التي تشغلها الدائرة على سطح مستوٍ، ويُمكن حساب مساحة الدائرة بالقانون التالي حيث يعتمد القانون بشكل أساسي على نصف قطر الدائرة : مساحة الدائرة= π × نصف القطر². ويُعبر عن الصيغة الرياضية بالرموز التالية: م= π × نق² إذ إنّ: م: مساحة الدائرة. π: قيمة ثابتة وتبلغ 3.14 أو 22/7. نق: نصف قطر الدائرة. تعد الدائرة من الأشكال الهندسية ، وهي شكل مغلق ينتج عن مجموعة من النقاط التي تبعد بمسافة ثابتة عن

قانون حجم الأسطوانة يمكن تعريف حجم الأسطوانة (بالإنجليزية: Cylinder Volume) بأنه كمية المادة التي توجد داخلها؛ فمثلاً يمثّل حجم الماء في بركة أسطوانية الشكل ممتلئة بالماء حجم هذه الأسطوانة أو البركة، وبالتالي فإنه يُمكن التعبير عن حجم الأسطوانة بالسعة أيضاً، ففي المثال السابق يمكن القول إن سعة البركة تساوي كمية أو حجم المياه اللازمة لملئها، ويُمكن حساب حجم الأسطوانة من خلال إيجاد حاصل ضرب مساحة قاعدتها في ارتفاعها، وذلك كما يلي: حجم الأسطوانة = مساحة القاعدة×الارتفاع= π×نق²×ع حيث إنّ: ع:

حساب مساحة نصف الدائرة يُمكن تعريف مساحة أي شكل هندسي على أنّه المساحة التي يشغلها الشكل على المستوى الثنائي الأبعاد، وكذلك الحال بالنسبة لمساحة نصف الدائرة التي يُمكن حسابها باستخدام القانون الآتي: مساحة نصف الدائرة= (π×مربع نصف قطر الدائرة)/2 وبالرموز: مساحة نصف الدائرة=(π×نق²)/2 حيثُ أنّ: نق: هو طول نصف قطر الدائرة . π: الثابت باي، وقيمته تساوي 3.14، 22/7. أمثلة متنوعة على حساب مساحة نصف الدائرة المثال الأول: جد مساحة نصف دائرة نصف قطرها= 7 سم، مع الأخذ بعين الاعتبار أن 22/7 = π؟ الحل:

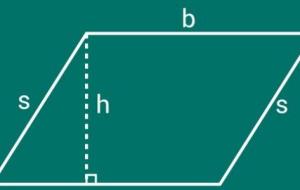
حساب مساحة متوازي الأضلاع باستخدام طول القاعدة والارتفاع تعرف مساحة متوازي الأضلاع (بالإنجليزية: Area of Parallelogram)، بأنها الفضاء ثنائي الأبعاد الذي يُشغله متوازي الأضلاع أو عدد الوحدات المربعة التي يغطيها متوازي الأضلاع، كما يمتلك متوازي الأضلاع العديد من الخصائص التي تميزه عن باقي الأشكال الهندسية، فهو أحد الأشكال الرباعية التي يكون فيها كل ضلعين متقابلين متساويين ومتوازيين، وكلّ زاويتين متقابلتين قياسهما متساوٍ أيضًا. يمكن حساب مساحة متوازي الأضلاع من خلال معرفة كل من طول قاعدته

قانون حساب مساحة سطح الكرة اكتُشفت صيغة قانون مساحة سطح الكرة منذ ألفيّ عام على يد الفيلسوف اليوناني أرخيميدس (بالإنجليزية: Archemedes)، حيثُ وجد أنّ مساحة سطح الكرة تساوي مساحة الجدار المنحني لأصغر اسطوانة بإمكانها أن تحتوي الكرة، كما أنّ مساحة سطح الكرة تساوي أربعة أضعاف مساحة الدائرة التي لها نفس نصف القطر ( مساحة الدائرة = π×نق²)، وعليه يمكن حساب مساحة سطح الكرة باستخدام القانون الآتي: مساحة سطح الكرة= 4×π×نق² حيثُ أنّ: نق: نصف قطر الكرة. π: باي، ثابت عددي قيمته 3.14 أو 22/7. كما يُمكن

كيفية حساب مساحة المخروط عند حساب مساحة المخروط أو حجمه فإن المخروط الذي يتم اعتباره لحساب مساحته أو حجمه لتطبيق القوانين عليه هو المخروط القائم وليس المائل، وهو الذي يمتلك قاعدة دائرية ويكون فيه الخط الواصل بين مركز القاعدة ورأس المخروط عمودياً على القاعدة، ويمكن إيجاد المساحة الكلية للمخروط من خلال إيجاد مجموع مساحة القاعدة، والمساحة الجانبية، وفيما يلي توضيح لكل منهما: مساحة القاعدة: تمثل مساحة الدائرة ؛ وذلك لأن القاعدة دائرية الشكل، وهي تساوي (π× نق )؛ حيث: نق: هو نصف القطر. المساحة

 كيفية حساب مساحة المثلث متساوي الساقين يمكن تعريف المثلث متساوي الساقين من خصائصه فهوالمثلث الذي يحتوي على ضلعين على الأقل من أضلاعه متساويين في الطول، ويمكن إيجاد مساحة المثلث متساوي الساقين من خلال مجموعة من القوانين، هي: استخدام القانون العام يمكن حساب مساحة المثلث متساوي الساقين من خلال القانون العام لمساحة المثلث ، وهو: مساحة المثلث متساوي الساقين = 1/2×القاعدة×الارتفاع وبالرموز: م= 1/2×ق×ع حيث: م: مساحة المثلث متساوي الساقين. ق: طول قاعدة المثلث. ع: ارتفاع المثلث. عند معرفة طول قاعدة

مساحة المثلث قائم الزاوية يُعرف المثلث قائم الزاوية Right Angled Triangle بأنه مثلث يحتوي على زاوية بقياس 90ْ درجة أي زاوية قائمة، وتكون هذه الزاوية محصورة بين الضلع القائم وقاعدة المثلث، بينما يمثل ضلعه الثالث الوتر، ومن المعروف أن مجموع زوايا المثلث يساوي 180ْ درجة، أي أن مجموع الزاويتين المتبقيتين يساوي 90ْ درجة، ويمتاز عن غيره من المثلثات بارتباط أضلاعه بصيغة رياضية تُدعى صيغة فيثاغورس وهي قانون المثلث قائم الزاوية، والصيغة التالية توضح صيغة مثلث قائم الزاوية على اعتبار أن المثلث س ص ع

طرق حساب مساحة القطاع الدائري يتم التعبير عادة عن مساحة الدائرة كاملة بالقانون: π×نق² ، وعندما يتطلب الأمر حساب مساحة جزء من الدائرة فإن ذلك يتم من خلال زاوية القطاع الدائري، ولأن قياس زوايا الدائرة كاملة يساوي 360 درجة، فإن نسبة زاوية القطاع الدائري إلى 360 درجة تتناسب مع مساحة الجزء من الدائرة المراد قياس مساحته. وبشكل عام تعتمد مساحة القطاع الدائري في أي دائرةٍ على الزاوية المركزيّة لهذا القطاع؛ فكلما زادت الزاوية المركزية له زادت زادت مساحة القطاع، وكلما نقصت قلت مساحته، كما تتناسب طردياً

قوانين حساب مساحة الأسطوانة يُمكن تعريف الأسطوانة على أنّها جسم ثلاثي الأبعاد يتكون من دائرتين مُتّصلتين مع بعضهما البعض لتشكيل شكل شبيه بالعمود المستدير، وتتمثّل مساحة سطحها بمجموع مساحة الدائرتين أو القاعدتين العلويّة والسفليّة، ومساحة المستطيل الجانبيّ الملتف بين القاعدتين، والذي يمثل المساحة الجانبية لها، وصيغة قانون المساحة لكلّ منهما هو كالآتي: مساحة الدائرة أو قاعدة الأسطوانة= π×نق² مساحة المستطيل أو المساحة الجانبيّة للأسطوانة= 2×π×نق×ع وبالتالي يكون القانون العام للمساحة الكليّة لسطح

حساب محيط نصف الدائرة باستخدام القانون يُمكن تعريف نصف الدائرة (بالإنجليزية: Semicircle) على أنه الشكل الناتج من قطر الدائرة والقوس الواصل بين طرفيه، ويُمكن تعريف المحيط لأي شكل ثنائي الأبعاد بشكل عام على أنه طول الخط الخارجي المحيط بالشكل. ويجدُر بالذكر هنا أن محيط نصف الدائرة لا يعادل في قيمته قيمة نصف محيط الدائرة كاملة؛ حيث يتمثّل محيط نصف الدائرة بمحيط نصف الدائرة الكاملة والذي يُمكن حساب قيمته عن طريق ضرب طول نصف القطر بالثابت باي، وبالرموز: πنق، إضافة إلى طول القطر الموجود أسفله، والذي

حساب محيط متوازي المستطيلات يعد متوازي المستطيلات شكل من الأشكال ثلاثية الأبعاد ، ويعتمد حساب محيطه على طوله وعرضه وارتفاعه وبما أنّ فيه 12 ضلعًا، فيُمكن حسابه بالصيغة الرياضية الآتية: محيط متوازي المستطيلات = 4 × (الطول العرض الارتفاع) وبالرموز: م = 4 × (س × ص × ع) حيث أنّ: م: محيط متوازي المستطيلات. س: طول متوازي المستطيلات. ص: عرض متوازي المستطيلات. ع: ارتفاع متوازي المستطيلات. يُعوض في القانون مباشرةً عندما تكون أطوال أبعاده معلومة. أمثلة على حساب محيط متوازي المستطيلات وفيما يلي بعض

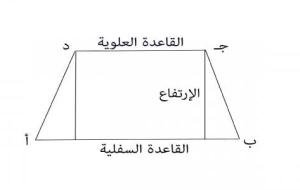
يمكن إيجاد محيط شبه المنحرف عن طريق مجموعة من القوانين ، وهي: حساب محيط شبه المنحرف من أطوال أضلاعه محيط شبه المنحرف يساوي مجموع أطوال أضلاعه، وبالرموز: محيط شبه المنحرف = أ ب جـ د ؛ حيث: أ، ب،ج، د: أضلاع شبه المنحرف. حساب محيط شبه المنحرف من ارتفاعه محيط شبه المنحرف= القاعدة العلوية القاعدة السفلية الارتفاع×((1/جا زاوية القاعدة اليمنى) (1/جا زاوية القاعدة اليسرى)). وبالرموز: محيط شبه المنحرف= أ ب ع×((1/جاس) (1/جا ص))، حيث: أ، وب: هما قياس الضلعين المتقابلين، والمتوازيين في شبه المنحرف. ع:

قانون حساب محيط ربع الدائرة يشكّل محيط ربع الدائرة المسافة المحيطة به من الخارج، ويتشكّل محيط ربع الدائرة من جزءٍ منحنٍ وجزأين مستقيمين، لذلك يُمكن الوصول إلى قانون حسابه بعدّة خطوات تتلّخص بما يأتي: حساب محيط الجزء المنحني الذي يساوي ربع محيط دائرة كاملة، ويساوي نتيجة قسمة محيط الدائرة كاملة على على العدد (4) ، كما يأتي: ¼×(2πنق). تبسيط المسألة للحصول على محيط الجزء المنحني وهو: (πنق)/2. حساب طول الجزأين المستقيمين وكلاهما أنصاف أقطار للدائرة وطولهما نق، للحصول على طول الجزء المستقيم وهو:

قانون محيط المعين المعين هو أحد الأشكال الرباعية ، لأن له أربعة أضلاع متساوية، وأربع زوايا لا يُشترط لقياساتها أن تكون 90 درجة، ويعرف محيط المعين (بالإنجليزية: Perimeter of Rhombus) بأنه المسافة الكلية التي تحيط بالشكل الخارجي، وبشكل عام يُعطى محيط المعين بالعلاقات الآتية: قانون حساب محيط المعين باستخدام طول الضلع حساب محيط المعين باستخدام طول الضلع: محيط المعين = 4 × طول الضلع. وبالرموز ح=4×ل؛ فجميع أضلاع المعين متساوية؛ حيث: ل: طول ضلع المعين. قانون حساب محيط المعين باستخدام طول القطرين حساب

قانون محيط المستطيل يمكن تعريف محيط المستطيل (بالإنجليزية:Perimeter of a Rectangle) على أنّه الطول الكلي لجميع أضلاع المستطيل، وبالتالي فهو يمثّل حاصل جمع كافة أضلاع المستطيل والتي يبلغ عددها 4 أضلاع، ، ومحيط المستطيل يساوي حاصل جمع أطوال أضلاع المستطيل، و يمكن حساب محيط المستطيل من خلال تطبيق الصيغة التالية: المحيط= الطول الطول العرض العرض. وبما أنّ من خصائص المستطيل أنّ كل ضلعين متقابلين متساويين؛ فإنّ محيط المستطيل= 2 × العرض 2× الطول. ويؤخذ العدد 2 كعامل مشترك ليُصبح المحيط = 2 × (العرض