تعليم

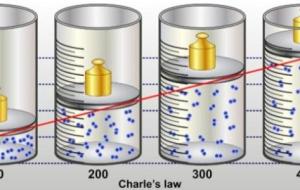
ما هو قانون شارل؟ ينص قانون شارل على أنّ حجم كمية معينة من الغاز تحت ضغط ثابت تتناسب تناسبًا طرديًا مع درجة حرارة الغاز المطلقة، بعبارةٍ أخرى هي دراسة العلاقة التي تربط درجة الحرارة وحجم الغاز عند تثبيت عامل الضغط، وسُميت العلاقة بهذا الاسم نسبةً إلى العالم الفيزيائي شارل. يُمكن تمثيل قانون شارل عن طريق الصيغة الرياضية الآتية: حجم الغاز / درجة حرارة الغاز = ثابت وبالرموز: ح / د = ث حيث إنّ: ح: حجم الغاز ويُقاس بوحدة مل. د: درجة حرارة الغاز وتُقاس بوحدة كلفن. ث: ثابت الغاز، ويُحدّد لكل عينة من

قانون قياس سرعة الضوء بما أنّ للضوء طبيعةَ الموجات الكهرومغناطيسيّة، فيمكن قياس سرعة الضوء باستخدام المعادلة الآتية: سرعة الضوء = الطول الموجي × التردد؛ وبالإنجليزية: Speed of Light = Wavelength × Frequency وبالرّموز: س ض = ط × ت؛ وبالإنجليزية: C = λ × F وبما أنّ التردد = 1 / الزمن؛ وبالإنجليزية: Frequency = 1 / Time وبالرّموز: ت = 1 / ز؛ وبالإنجليزية: F = 1 / T فإنّه يمكن التعبير عن سرعة الضوء بالصيغة الآتية: سرعة الضوء = الطول الموجي / الزمن؛ وبالإنجليزية: Speed of Light = Wavelength / Time

ما هو قانون سرعة التفاعل ينص قانون سرعة التفاعل (بالإنجليزية: Reaction Rate Law) على التغير في تركيز المواد المتفاعلة مع مرور الزمن، بحيث يقل تركيز المواد المتفاعلة، ويزيد تركيز المواد الناتجة مع مرور الزمن وسير التفاعل، وتتغير سرعة التفاعل بتغير تركيز المواد المتفاعلة فقط، أي أنّ سرعة التفاعل ليس لها علاقة بتركيز المواد الناتجة، إذ يُبين قانون سرعة التفاعل العلاقة بين سرعة التفاعل وتركيز المواد المتفاعلة أو ضغوطها الجزئية، ويُمكن تمثيله بالصيغة الرياضية الآتية: سرعة التفاعل= ثابت التفاعل ×

ما هو قانون ستيفان بولتزمان؟ ينص قانون ستيفان بولتزمان على أنَّ الطاقة الكاملة المنبعثة من الجسم الأسود بوحدة واط في الثانية لكل وحدة مساحة تتناسب مع القوة الرابعة لدرجة حرارة الجسم المطلقة بوحدة كلفن، إذ يصف القانون قدرة الجسم على امتصاص الأشعة الساقطة على سطحة عند درجة حرارة معينة، والجسم الذي له قدرة فعالة جدًا على امتصاص وانبعاث الأشعة هو الجسم الأسود، وكلما زادت سخونة ودرجة حرارة الجسم الأسود، زاد إشعاعه. معنى الجسم الأسود في قانون ستيفان بولتزمان يعبّر الجسم الأسود عن حالةٍ مثاليَّة

قانون حفظ الزحم يُعدّ قانون حفظ الزخم أو حفظ كمية الحركة (بالإنجليزية: Conservation of momentum) من القوانين الفيزيائية التي تُعبّر عن الثبات في كمية الزخم لمادةٍ ما عند تعرّضها لمجموعة من الظروف والعوامل، أيّ أنّ الزخم الكلي لنظام ما يظل دائماً ثابت، ويُشير قانون الزخم إلى كتلة الجسم مضروبة في سرعته بحيث تُعادل القوة المطلوبة لإيقاف الجسم في وحدة الزمن، ويُساوي الزخم لمجموعة من الأجسام مجموع العزم الفردي لكل جسم، ويُعد الزخم كمية متجهة؛ أي أنّ له قيمة واتجاه حركة، وعليه يكون إجمالي العزم

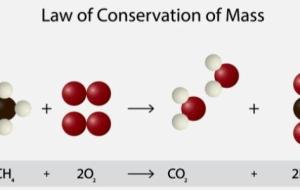
تعريف قانون حفظ المادة ينصّ القانون العام لحفظ المادة أو حفظ الكتلة (بالإنجليزية: Law of Conservation of Mass) على أنّ المادة في النظام المغلق لا يمكن أن تفنى ولا تُستحدث، ولكن تبقى محفوظة وتتحول من شكل إلى آخر، والمقصود بالنظام المغلق هو النظام الذي لا تتفاعل به المادة مع ما يُحيط بها. ومن الجدير بالذكر أنّه وبعد التوصل إلى قانون حفظ المادة عُدّل عليه وطُوّر من قِبل العلماء في مجال الكيمياء ومجال الميكانيكا، وأصبح القانون قابلًا للتطبيق في مجال الكيمياء والفيزياء. قانون حفظ المادة في الكيمياء

نص قانون حفظ الطاقة يُعدّ قانون حفظ الطاقة (بالإنجليزية: Energy)، أو مبدأ بقاء الطاقة من أهم القوانين الفيزيائية، والذي ينص على أنّ " الطاقة لا تختفي ولا تتلاشى ولا تنشأ من لا شيء؛ بل تتحول من شكل إلى آخر، وهذا يعني أنّ الطاقة الكلية للنظام المعزول تبقى ثابتة ولا تنتهي، و الطاقة الموجودة في الأجسام متعددة ومنها؛ الطاقة الحركية، والطاقة الحرارية، والطاقة الكهربائية، والطاقة الميكانيكية. وحيث أنّ الكتلة والطاقة مفهومان متشابهان، فكل جسم يمتلك طاقة تتناسب مع كتلته، و يمكن لأيّ كتلة أن تتحول إلى

معادلة حساب شدة المجال المغناطيسي حساب شدة المجال المغناطيسي لسلك طويل مستقيم يُمكن حساب شدة المجال المغناطيسي الناتج كخطوط مغلقة وملتفة حول سلك مستقيم وطويل يسري فيه تيار كهربائي بالصيغة الرياضية التالية: شدة المجال المغناطيسي = (ثابت النفاذية المغناطيسة × شدة التيار الكهربائي) / (2 × π × المسافة الفاصلة بين النقطة المُراد حساب شدة مجالها والسلك) ويُمكن تمثيلها بالرموز: (2πr) / (I × μo) = B حيث أنّ: B: شدة المجال المغناطيسي ويُقاس بوحدة تسلا (T). I: شدة التيار الكهربائي المار بالسلك ويُقاس

قانون حساب حجم المخروط يمكن التعبير عن قانون حجم المخروط وِفقاً لنوعه، وذلك من خلال ما يأتي: قانون حجم المخروط القائم يُمكن حساب حجم المخروط القائم من خلال القانون الرياضي الآتي: حجم المخروط القائم= 1 /3 × مساحة القاعدة × الارتفاع وبالرموز: حجم المخروط القائم= 1/ 3× π × نق²× ع ملاحظة: كُتب القانون بهذا الشكل لأنّ مساحة القاعدة الدائرية = π× نق² حيث إنّ: نق: نصف قطر القاعدة الدائرية. ع: ارتفاع المخروط القائم. π: ثابت عددي، وقيمته 3.14 أو 22/ 7. قانون حجم المخروط الناقص يُمكن التعبير عن حجم

معادلة حساب القدرة الكهربائية يُمكن تعريف القدرة الكهربائيّة (بالإنجليزية:Electric Power) على أنّها الشّغل المبذول أو الطاقة الكهربائيّة المُستَهلَكة في الدّارة الكهربائيّة في وحدة من الزمن، ولهذا فإنّ المعادلة الرئيسيّة التي تعبّر عن القدرة الكهربائيّة هي كما يأتي: القدرة الكهربائية = الشغل / الزمن. وبالرّموز: القدرة = ش / ز ويُمكن استنتاج عدّة علاقات تُستخدم لحساب القدرة الكهربائيّة من المعادلة السابقة، كما يأتي: يُمكن التعبير عن الشغل (ش) بدلالة الجهد الكهربائي (جـ) والشحنة الكهربائيّة (شـ)

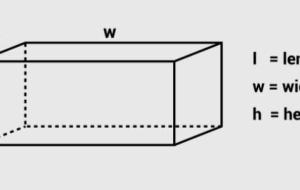
كيفية حساب حجم متوازي المستطيلات يمكن حساب حجم متوازي المستطيلات الذي يعتبر شكلاً ثلاثي الأبعاد من خلال القانون الآتي: حجم متوازي المستطيلات= الطول×العرض×الارتفاع وبالرموز: ح=أ×ب×جـ حيث أن: ح: حجم متوازي المستطيلات. أ: طول متوازي المستطيلات. ب: عرض متوازي المستطيلات. جـ: ارتفاع متوازي المستطيلات. أمثلة متنوعة على حساب حجم متوازي المستطيلات وفيما يأتي بعض الأمثلة على حساب حجم متوازي المستطيلات: المثال الأول: ما هو حجم متوازي المستطيلات الذي طوله 14سم، وعرضه 12سم، وارتفاعه 8سم؟ الحل: حجم متوازي

قانون حساب حجم المكعب يمكن حساب حجم المكعب بطريقتين مختلفتين وهما كالآتي: عند معرفة طول الضلع بما أنّ أضلاع المكعب أو حوافه متساوية في الطول، فيمكن حساب الحجم باستخدام الصيغة الآتية: حجم المكعب= (طول الضلع)³. وبالرموز: ح = أ³ حيث أنّ: ح: حجم المكعب. أ: طول ضلع المكعب. عند معرفة طول القطر يمكن حساب حجم المكعب عند معرفة طول القطر من خلال المعادلة الآتية: حجم المكعب= (طول القطر)³ × 3/9√ وبالرموز: ح = (ق)³ × 3/9√ حيث أنّ: ح: حجم المكعب. ق: طول قطر المكعب. أمثلة على حساب حجم المكعب وفيما يأتي أمثلة

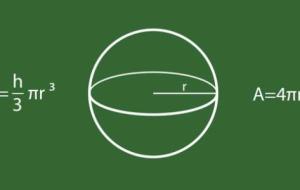
قانون حساب حجم الكرة يُمكن تعريف حجم الكرة (بالإنجليزية: Sphere Volume) أو الجسم الصلب ثلاثي الأبعاد بأنها كمية الفراغ الموجودة داخل الجسم، ويُقاس بالوحدات المكعّبة، ويُمكن إيجاد حجم الكرة عن طريق العلاقة الآتية: حجم الكرة= 4/3×π×مكعب نصف القطر، وبالرموز: ح=4/3×π×نق³ حيث إنّ: ح: حجم الكرة. نق: هو نصف قطر الكرة. π: الثابت باي وتعادل قيمته تقريباً 3.14. من الجدير بالذكر هنا أيضاً هو أنّ حاصل الضرب (4/3×π) يساوي تقريباً القيمة: 4.19، لذلك يمكن كتابة القانون السابق على شكل حجم الكرة= 4.19×نق³.

نص قانون جول ينص قانون جول على أنَ: "الطاقة الحرارية الناتجة في مقاومة ما بسبب مرور تيار كهربائي فيها تتناسب طرديًا مع القدرة الكهربائية والمدة الزمنية التي يسري فيها التيار". فقانون جول عبارة عن وصفٍ لمعدل تحويل المقاومة في الدائرة الكهربائية إلى طاقةٍ حرارية، حيثُ أن كمية الحرارة في الثانية التي تنشأ في سلك يحمل تيارًا يتناسب مع المقاومة الكهربائية للسلك ومربع شدة التيار، فكمية الحرارة المتصاعدة تعادل الطاقة الكهربائية المفقودة. وقد اكتشف قانون جول العالم الفيزيائي الإنجليزي جيمس بريسكوت جول

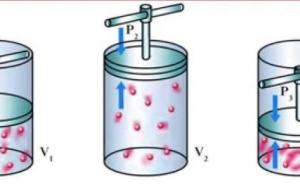
قانون جاي لوساك للغازات ينصّ قانون جاي لوساك للغازات على أنّه عندما تزداد درجة حرارة عينة من الغاز في عبوة صلبة فإنّه سيزداد ضغط الغاز، فالزيادة في الحرارة ستزيد الطاقة الحركية لجزيئات الغاز، ممّا يجعلها تتصادم في جدران هذه العبوة بقوّة كبيرة، وهذا ما يُفسر زيادة الضغط، واكتشف هذا الأمر الكيميائي الفرنسي جوزيف جاي لوساك عند دراسة العلاقة بين ضغط الغاز ودرجة حرارته المطلقة، كما أنّ ضغط كتلة الغاز يختلف مع اختلاف درجة الحرارة المطلقة، ويُشبه هذا القانون قانون تشارلز لكن الفرق في نوع العبوة، ففي

قانون جاوس المغناطيسي يَنص قانون جاوس المغناطيسي على أنّ: التدفق المغناطيسي الكلي عبر سطح مغلق يُساوي دائمًا صفر، أي أنّ الأقطاب لا يُمكن أن تَكون أحادية (قطب سالب فردي) بل زوجية (كل قطب موجب يقابله قطب سالب)، سُمي القانون بجاوس نسبةً إلى العالم جاوس ، والصيغة الرياضية للقانون تعتمد على نظريات التفاضل والتكامل في الرياضيات. الصيغة الرياضية لقانون جاوس المغناطيسي   يُمكن التعبير عن قانون جاوس المغناطيسي بإحدى الصيغ الرياضية الآتية: صيغة التكامل يُعبر عن قانون جاوس المغناطيسي بصيغة التكامل

قوانين تحويل درجات الحرارة تتعدد مقاييس درجة الحرارة المُستخدمة، وهناك 3 مقاييس مُستخدمة في الوقت الحالي، وهي كالآتي: وحدة القياس بالإنجليزية الرمز النظام فهرنهايت Fahrenheit F البريطاني درجة الحرارة المئوية Celsius C المتري كلفن Kelvin K المتري النظام المتري: هو النظام الدولي المُعتمد للأوزان والمقاييس في جميع أنحاء العالم تقريبًا، ويستخدم وحدات مثل: المتر والكيلوغرام، كما أنّه الأساس الذي بُني عليه النظام العالمي للوحدات (SI). النظام البريطاني: يُعرف أيضًا بالنظام الإمبراطوري، واستُخدم في

قانون تحويل الفهرنهايت إلى درجة مئوية تُعرف درجة الفهرنهايت (بالإنجليزية: Fahrenheit) على أنّها إحدى وحدات القياس المُستخدمة لقياس درجة الحرارة في النظام الإنجليزي، ويرمز لها بالرمز (F)، وقد وضعها العالم الفيزيائي الألمانيّ دانيال غابرييل فهرنهايت عام 1724م. أمّا الدرجة المئوية (بالإنجليزية: Centigrade) أو ما يُعرف بدرجة السيليسيوس (بالإنجليزية: Celsius) ويرمز لها بالرمز (C)، فهي إحدى وحدات القياس المُستخدمة لقياس درجة الحرارة في النظام المتري، أو النظام الدولي للوحدات. أما قانون تحويل

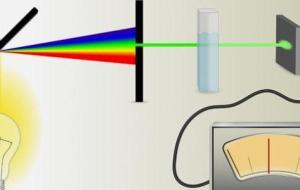
قانون بير لامبرت يعد قانون بير لامبرت (بالإنجليزية: Beer–Lambert law) والذي يعرف أيضًا بقانون بير، وقانون لامبرت بير، وقانون بير لامبرت بوغوير أحد أهمّ قوانين علم البصريات. ويوضح القانون العلاقة التجريبية التي تربط بين امتصاص الضوء وخصائص الوسط الممتص على ضوء دراسة بير المتعمقة لشدة الضوء، فطوّر النظرية التي تنص على أن العين لا تستطيع تحديد مقدار السطوع، ليستطيع أن يثبت أن العين وبالرغم من ذلك تستطيع اكتشاف فرق السطوع بين جسمين، ليصبح بذلك مؤسس القياس الضوئي. تجدر الإشارة إلى أن العالم بيير

نص قانون بويل في الفيزياء يُعرّف قانون بويل أيضاً بقانون ماريوت، ويُوضّح القانون العلاقة ما بين الضغط وتمدّد الغاز عند درجة حرارة ثابتة، حيث أوجد العالِم الفيزيائي روبرت بويل قانون بويل الذي ينصّ على أنّ العلاقة بين الضغط لكمية معيّنة من الغاز تتناسب عكسياً مع حجمه عند درجة حرارة ثابتة. يُشير قانون بويل إلى العلاقة العكسية بين حجم كتلة معيّنة من الغاز والضغط الواقع عليه، وذلك عند تثبيت درجة الحرارة، ويُمكن ملاحظة ذلك عند عملية الشهيق، حيث يزداد حجم الرئة وينخفض الضغط فيها في نفس الوقت، ونتيجةً

ما هو قانون بويل؟ ينص قانون بويل على أنّ الضغط الذي تُمارسه كمية معينة من الغاز عند درجة حرارة ثابتة، يتناسب تناسبًا عكسيًا مع الحجم الذي يشغله الغاز، ويُمكن تمثيل هذه العلاقة بالصيغة الرياضية التالية: ضغط الغاز = 1 / حجم الغاز حجم الغاز × ضغط الغاز = ثابت وبالرموز: ض ∝ (1 / ح) ح × ض = ث إذ إنّ: ح: الحجم الذي يشغله الغاز، ويُقاس بوحدة اللتر. ض: ضغط الغاز، ويُقاس بوحدة الضغط الجوي (باسكال). ث: ثابت الغاز. وممّا سبق يتّضح أنّ قانول بويل يدرس العلاقة بين ضغط الغاز وكتلته عند درجة حرارة ثابتة، أي

ما هو قانون بلانك قانون بلانك هي علاقة رياضية صاغها العالم ماكس بلانك سنة 1900م، وكان هدفه شرح كيفية توزيع الطاقة الطيفية للإشعاع المنبعث من الجسم الأسود، والجسم الأسود هو جسم افترضي يمتص كافة الطاقة الإشعاعية التي تسقط عليه، ويصل لدرجة حرارة التوازن، ويعيد إرسال الطاقة مرة أخرى بسرعة أكبر من الطاقة التي يمتصها، ولقد افترض العالم بلانك أن مصادر الإشعاع هي الذرات التي هي في حالة تذبذب مستمر، وتُصدر من تذبذبها طاقة اهتزازية. كما ويُعرف الجسم الأسود بأنه المُبرد المثالي الذي يمتص الإشعاعات التي

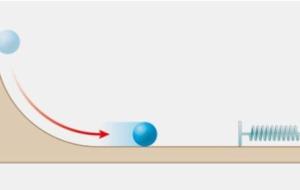
قانون حفظ الطاقة الميكانيكية وفقًا لقانون حفظ الطاقة الميكانيكية، فإن الطاقة لا تفنى ولا تُستحدث من عدم، بالرغم من أنه يُمكن تغييرها من شكل إلى آخر. لتوضيح الفكرة، فإن السيارة تكون ثابتة الحركة في أعلى تل، لكن عندما تهبط إلى أسفله فإنها تتحرك بشكل متسارع، وبالتالي تزداد طاقتها الحركية وتقل طاقة الوضع خاصتها، وعندما تصعد إلى أعلاه فإنها ستحول الطاقة الحركية التي اكتسبتها إلى طاقة وضع، وعند إهمال تأثير الاحتكاك ، فإن السيارة ستصل إلى نفس الارتفاع الذي بدأت منه. يُعبر عن قانون حفظ الطاقة

مبدأ برنولي للطيران ينص مبدأ برنولي على أنّ ضغط الهواء يقل مع زيادة سرعة تدفقه، ويزداد مع تناقص سرعة تدفقه ، ولذلك عندما يتحرك الهواء بسرعة، فإنّه يُشكل منطقة منخفضة الضغط بسبب انتشار الجزيئات وتباعدها عن بعضها بعضًا، بينما عندما يتحرك بسرعة أقل، فإنّه يُشكل منطقة ذات ضغط مرتفع، لأنّ الجزئيات تكون متقاربة جدًا من بعضها بعضًا. يُفسر مبدأ برنولي قوة الرفع التي تدفع الطائرة للطيران والناتجة من شكل جناح الطائرة، إذ يُصمم جناح الطائرة ليكون الجزء العلوي منه منحني، وبالتالي فإنّ الهواء يتحرك فوقه