تعليم

نص قانون براغ ينص قانون براغ على أنّه؛ "عند سقوط حزمة من الأشعة السينية على سطح بلوري، فإنّ زاوية سقوط الأشعة على السطح البلوري تساوي زاوية تشتت وانتشار الأشعة من السطح البلوري، وعندما يكون هناك فرق في طول المسار بين الأشعة المنعكسة عن طبقات الذرات المكونة للمادة يساوي تقريبًا الطول الموجي للأشعة المنعكسة فإنّه يحدث تداخلًا بناء للموجات مع بعضها البعض ويُسمى هذا التداخل بحيود براغ". يُعد قانون براغ حالة خاصة من حالات حيود لاو، ويشرح القانون علاقة سقوط أشعة سينية على سطح بلوري وكيفية انعكاسه،

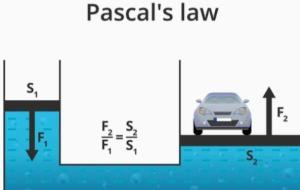
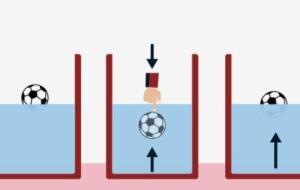
نص قانون باسكال للضغط ينصّ مبدأ أو قانون باسكال (بالإنجليزية: Pascal's Law ) على أنّ الضغط المطبّق على سائل محصور ينتقل بشكلٍ موحّد في جميع الاتجاهات على جميع أنحاء السائل بصرف النظر عن شكل الوعاء، أي أنّ تغيّر الضغط في جزء واحد من السائل ينتقل لجميع الأجزاء الأخرى من السائل وإلى جدران الوعاء، وقد أعلن العالم الفرنسي بليز باسكال هذا القانون لأول مرّة في العالم، ووفقًا لهذا القانون يُنتج الضغط الذي يُمارس على المكبس زيادة مساوية في الضغط على مكبس آخر في النظام الهيدروليكي. الصيغة الرياضية

ما هو قاون باسكال قام العالم باسكال بالعديد من التجارب على الموائع أو السوائل المحصورة، فتساءل باسكال عن ما الذي يحدث عندما نقوم ببذل ضغط خارجي على مائع محصور، وأنّه كيف سيكون سلوك هذا المائع، فوجد باسكال أنّه عندما نبذل ضغطاً خارجياً على مائع محصور فإّن ضغط هذا المائع يزداد بمقدار الضغط الخارجي الواقع عليه، وبالتالي فإنّ ضغط هذا المائع سوف يزداد على جدران الوعاء الموجود فيه وينتقل إلى جميع أجزاء الوعاء بنفس المقدار. وسمّيت هذه الظاهرة بمبدأ باسكال والذي ينص على أنّه إذا وقع ضغط خارجي على مائع

قانون الوزن النوعي يُعرف الوزن النوعي (Specific Weight) أيضًا بوزن الوحدة ويُعرّف بأنّه وزن المادة لكل وحدة حجم لهذه المادة، ويُرمز له بالرمز غاما (γ)، ويُمثل الوزن القوة ولذلك يُقاس بالنظام العالمي للوحدات أو النظام الدولي للوحدات (SI) بوحدة نيوتن / م³، بينما يُقاس بالنظام البريطاني الإمبراطوري بوحدة باوند/قدم³، ويُمكن حسابه من خلال الصيغة الرياضية الآتية: الوزن النوعي = وزن المادة / وحدة الحجم وبالرموز: و ن = و / ح وبالرموز الإنجليزية: γ = W/V حيث إنّ: و ن (γ): الوزن النوعي للمادة، ويُقاس

حساب النسبة المئوية النسبة المئوية هي نسبة جزء من مائة من كمية ما، هذا يعني أن الكمية الكلية دائماً تعتبر 100 وتوضع في مقام الكسر، أما قيمة البسط فهو مقدار قيمة الجزء بالنسبة للمائة، ونتيجة قسمتهما تشير إلى قيمة توضح العلاقة بين الجزء والكل، كما هو موضح في العلاقة الآتية: النسبة المئوية = (الجزء / القيمة الكلية) × 100 إذ إن: الجزء: القيمة المراد تحديد نسبتها. القيمة الكلية: المجموع الكلي للقيم. والنسبة المئوية هي قيمة لا وحدة لها، والسبب في ذلك أن القيمة الجزئية والقيمة الكلية كميتين من نفس

قانون المسافة في الفيزياء تُعرّف المسافة (بالإنجليزية: Distance) في الفيزياء بأنها الخط الواصل بين نقطتين (شيئين أو شخصين)، أو المقدار الذي يتحركه جسم معين من مكانٍ إلى آخر، أما وحدة المسافة فهي السنتيمتر أو المتر أو الكيلومتر وفقًا للنظام العالمي للوحدات، ويمكن حساب المسافة باستخدام القانون الموضح أدناه: المسافة = السرعة × الزمن. وبالرموز: م = ع × ز. إذ إنّ: م: رمز المسافة بوحدة المتر (م). ع: رمز السرعة بوحدة متر/ ثانية (م/ث). ز: رمز الزمن بوحدة الثانية (ث). قانون المسافة في الرياضيات تُعرّف

قوانين المساحة لأهم الأشكال ثنائية الأبعاد قانون مساحة المربع مساحة المربع = (الضلع)^2 وبالرموز: م = س × س حيث أنّ: س: هي طول ضلع المربع مثال: إذا كان طول ضلع المربع 5 سم، فإن مساحة المربع تساوي: الحل: مساحة المربع = (5) = 25 سم قانون مساحة المستطيل مساحة المستطيل = حاصل ضرب الطول في العرض وبالرموز: م = س × ص حيث أنّ: م: مساحة المستطيل س: طول المستطيل ص: عرض المستطيل مثال: إذا كان طول المستطيل 4 سم، وعرضه 3 سم، فإن مساحة المستطيل تساوي: الحل: مساحة المستطيل = 4 × 3 = 12سم قانون مساحة المثلث

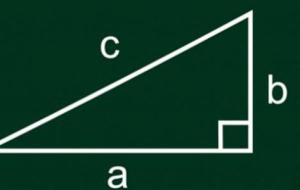
نص قانون المثلث القائم يُعرف المثلث قائم الزاوية (بالإنجليزية: Right Angled Triangle) بأنه مثلث ذو زاوية بقياس 90ْ درجة، وتكون هذه الزاوية محصورة بين الضلع القائم وقاعدة المثلث، بينما يمثل ضلعه الثالث الوتر. ومن المعروف أن مجموع زوايا المثلث يساوي 180ْ درجة، أي أن مجموع الزاويتين المتبقيتين يساوي 90ْ درجة، ويمتاز عن غيره من المثلثات بارتباط أضلاعه بصيغة رياضية تُدعى نظرية فيثاغورس وهي قانون المثلث قائم الزاوية. والصيغة الرياضية الآتية توضح قانون المثلث قائم الزاوية على اعتبار أن المثلث س ص ع

قانون الكثافة النسبية لفظًا تُعرف الكثافة النسبيّة (Relative Density) بأنّها النسبة بين كمية كثافة المادة بالنسبة لكثافة مادة مرجعيّة، وغالبًا ما يكون الماء هو المادة المرجعيّة التي تُحسب الكثافة النسبيّة للمواد الأخرى بالنسبة له. قانون الكثافة النسبية رياضيًا تُعدّ الكثافة النسبيّة كمية فيزيائيّة بلا أبعاد لأنّها لا تمتلك وحدة فيزيائيّة، حيثُ تُحسب بقسمة كثافة على كثافة أخرى، وبالتالي تتمثل الكثافة النسبيّة من خلال الصيغة الرياضيّة الآتية: الكثافة النسبية = كثافة المادة / كثافة الماء

ما هو قانون الكتلة تُعرَّف الكتلة (بالإنجليزية: Mass) على أنّها خاصية فيزيائية تُشير لما يحويه الجسم من مادة، ومقدار مقاومة تسارع هذه المادة، ويُمكن استخدام الكتلة في تحديد درجة الحرارة؛ والضغط؛ وسمات المواد الصلبة؛ والسائلة؛ والغازات، وهُنالك علاقة تجمع الكتلة بالحجم والكثافة. حساب الكتلة بالنسبة للوزن تُعبِّرُ الكتلة عن مقدار مادة ما يحتويها الجسم، أمّا الوزن فهو مقياس لمقدار القوة المؤثرة على جسم ما بواسطة الجاذبية، ودائمًا ما تتغير الجاذبية بناءً على موقع قياسها، فعلى سبيل المثال قوة

ما هو قانون القوة؟ تُعرّف القوة (بالإنجليزية: Force) بأنّها التفاعل الذي يؤثر على الأجسام، ويُغير من حركتها، وتنص صيغة القوة على أنّ القوة تساوي كتلة الجسم التي تؤثر عليه القوة مضروبة في تسارعه، ويُمكن تمثيل القانون بالصيغة الآتية: القوة = الكتلة × التسارع وتُمثل بالرموز: ق = ك × ت وبالإنجليزية: F = m x a حيث أنّ: ق (F): هي القوة المؤثرة على الجسم، وتُقاس بوحدة نيوتن (N). ك (m): هي كتلة الجسم، وتُقاس بوحدة (كغ). ت (a): هو تسارع الجسم، ويُقاس بوحدة (م/ث²). وتُمثل القوة بناءً على قوانين نيوتن

قوانين حساب القدرة الكهربائية تُعرف القدرة الكهربائية (بالإنجليزية: Electric power) على أنها الشغل المبذول في تحويل الطاقة من شكل إلى آخر ، إذ يُمكن حساب القدرة الكهربائية باستخدام العديد من القوانين. القوانين الأساسية لحساب القدرة الكهربائية يُمكن حساب القدرة الكهربائية باستخدام قانون يربط بين التيار والجهد، كما هو موضح في العلاقة الآتية: القدرة الكهربائية = الجهد الكهربائي × التيار الكهربائي وبالرموز: ق = ج × ت حيث إن: ق: القدرة الكهربائية (بالإنجليزية: Power)، وتُقاس بوحدة الواط. ج: الجهد

قانون القدرة يمكن حساب القدرة الكهربائية باستخدام القوانين الآتية: القدرة (P) = الطاقة اللازمة لإنجاز عمل ما (E) / الزمن (t) القدرة (P) = الشغل المنجز (W) / الزمن (t) تتمثل القدرة في العلاقة الآتية عند وجود تيار وجهد كهربائي: القدرة (P) = الجهد (V) * التيار (I) تتمثل القدرة في العلاقة الآتية عند وجود جهد كهربائي ومقاومة: القدرة (P) = (الجهد (V)) / المقاومة (R) تتمثل القدرة في العلاقة الآتية عند وجود تيار كهربائي ومقاومة: القدرة (P) = التيار (I) * (المقاومة (R)) تتمثل القدرة في العلاقة الآتية

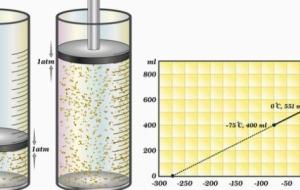
قانون الغازات المثالية يُعرف الغاز المثالي (بالإنجليزية: Ideal Gaz) بأنّه الغاز المكون من ذرات وجزيئات تتصادم مع بعضها بشكل مرن، دون وجود أيّ قوى جذب بين جزيئاتها، ودون حدوث أيّ تفاعل فيما بينها، كما تمتلك جزيئات أو ذرات الغاز المثالي طاقة حركية تتغير بتغير درجات الحرارة، ويُمثل القانون الآتي قانون الغاز المثالي: حجم الغاز × الضغط المطلق = ثابت الغازات العام × عدد المولات × درجة الحرارة المطلقة، وبالرموز؛ ح ض = ر ن د. ويكتب القانون بالرموز الأجنبية؛ P  × V = n  × R  × T = N  × k  × T؛ حيث إن

التعريف بقانون الطفو  يُعرّف الطفو (بالإنجليزية: buoyant force) بأنّه قوة تؤثر على الأجسام المغمورة في السوائل من خلال دفعها للأعلى، وينص مبدأ أرخميدس للطفو الذي اكتشفه العالم اليوناني أرخميدس على أنّ القوة المؤثرة على أي جسم ساكن مغمور كليًا أو جزئيًا في سائل أو غاز هي قوة تصاعدية تُعرف بقوة الطفو، وتساوي هذه القوة وزن السائل المُزاح من الجسم المغمور. ويساوي حجم السائل المُزاح حجم الجسم المغمور كليًا في السائل، أو حجم الجزء من الجسم المغمور جزئيًا في السائل، ويُعادل وزن جزء السائل المُزاح قوة

الطاقة الحركية يعتبر مفهوم الطاقة وأشكالها ومصادرها من أهم المفاهيم الفيزيائية التي لها تطبيقات كثيرة في مجالات الفيزياء التطبيقية والمسارعات النووية، وفي مجال التكنولوجيا و التطبيقات الهندسية وغيرها من المجالات العديدة، حيث اعتمدت عدد كبير من الدول على تحولات الطاقة لاستخدامها في المجالات الصناعية وتوليد الطاقة الكهربائية. وللطاقة أشكال كثيرة تتحول من شكل إلى آخر حسب الظروف المتوفرة والأداة المستخدمة لاستهلاك أو توليد الطاقة، ومن أشهر أنواع الطاقة التي نتعامل معها بشكل دائم ألا وهي الطاقة

ما هو قانون الطاقة الحرارية؟ يمكن تعريف الطاقة الحرارية (بالإنجليزية: Thermal energy) على أنّها طاقة يحصل عليها جسم أو نظام ما نتيجة حركة جزيئاته، وتمثل الطاقة الحرارية قدرة الشيء على العمل نتيجة حركة جزيئاته، وبما أنها ناتجة عن حركة الجزيئات يمكن تصنيفها كنوع من أنواع الطاقة الحركية (kinetic energy)، وتؤدي الطاقة الحراريّة إلى رفع درجة الحرارة الداخلية للجسم، وتقاس هذه الحرارة بوحدات الدرجة المئوية أو الفهرنهايت، ويُشار إلى أنّه كلما ازدادت سرعة حركة الجزيئات ازدادت درجة الحرارة المُسجلّة.

قانون الطاقة لآينشتاين تعد المعادلة التي تعرف بمعادلة تكافؤ المادة والطاقة، التي قدمها العالم ألبرت آينشتاين في أطروحته النظرية النسبية الخاصة ، من أشهر المعادلات، حيث تعبر عن حقيقة أن الكتلة والطاقة متكافئان، ومن الممكن أن يتحول أحدهما إلى الآخر. في النظريات السابقة -أو ما يعرف بالفيزياء الكلاسيكية- والتي سبقت النظرية النسبية الخاصة، كان يُنظر إلى الكتلة والطاقة على أنهما مختلفتان تمامًا، لا يمكن الربط بينهما بعلاقة رياضية. ولكن ما جاءت به النظرية النسبية الخاصة، هو الربط بين هذين المفهومين،

قانون باسكال للضغط وضع باسكال قانونًا للضغط سمّي نسبةً له بقانون باسكال، وركّز فيه على ضغط المواد السائلة تحديدًا، ويُعرف بناءً على ذلك بمبدأ انتقال ضغط السوائل أيضًا، وينص القانون عمومًا على أنّ الضغط الخارجي المطبّق على سائلٍ ما سيتوزّع بصورة متكافئة على جميع أجزائه وبكلّ الاتجّاهات، شرط أن يكون السائل محصورًا، وبذلك تكون قيمة الضغط عند أي نقطة في السائل متساوية. يُمكن التعبير عن قانون باسكال بالصيغة الرياضية الآتية: القوة الخارجية = الضغط المنتقل عبر السائل × مساحة المقطع العرضي ويُمكن

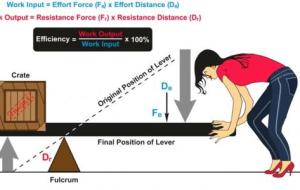
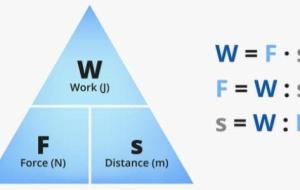
قانون الشغل في الفيزياء يُعبر الشغل في الفيزياء عن القوة الخارجية المُستخدمة لإزاحة جسم ما، وبالتالي فإنّ الشغل كمية قياسية ناتجة عن حاصل ضرب كميتين متجهتين وهما القوة الخارجية المؤثرة على الجسم، والإزاحة الناتجة عن تحريك الجسم، ويُقاس الشغل في النظام الدولي للوحدات بوحدة الجول (J)، ويُمكن تمثيل هذه العلاقة بالصيغة الرياضية الآتية: الشغل = القوة المؤثرة على الجسم × الإزاحة ويُستخدم هذا القانون إذا كانت الإزاحة في نفس اتجاه القوة المؤثرة على الجسم، أي أنّ الزاوية بينهما تساوي صفر، بينما إذا

حساب الشغل المبذول يمكن تعريف الشغل من خلال علاقته بالطاقة ، فهو مقدار الطاقة اللازمة لإزاحة الجسم لمسافة معينة بتطبيق قوة خارجية باتجاه هذه الإزاحة، ويُعد الشغل من القوانين الفيزيائية وهو حاصل ضرب الإزاحة التي يقطعها الجسم مع القوة المؤثرة عليه، وهو كمية قياسية يُقاس بوحدة الجول، ويُمكن حسابه بالصيغة الرياضية الآتية: الشغل المبذول على جسم = القوة المؤثرة × الإزاحة × جتا(الزاوية بين القوة والإزاحة) ويُمكن تمثيله بالرموز كالآتي: ش = ق × ف × جتاθ W = fd cos θ إذ إنّ: ش (W): الشغل المؤثر على

قانون حساب الزمن يُمكن حساب الزمن لجسم يتحرك باتجاه واحد من خلال العلاقة التي تجمع بين عاملي المسافة والسرعة، وهي: السرعة = المسافة / الزمن وبإعادة ترتيب المعادلة بحيث يُصبح الزمن هو موضع القانون وعلى النحو الآتي: الزمن = المسافة / السرعة ز= ف / ع حيث: ز: الزمن. ف: المسافة. ع: السرعة. يُمكن حساب الزمن المقطوع لجسمين متحركين في اتجاه واحد من خلال العلاقة الآتية: ز= ف / (ع1 - ع2)، حيث ع1 > ع2 حيث: ز: الزمن. ف: المسافة. ع1: سرعة الجسم الأول. ع2: سرعة الجسم الثاني. يُمكن حساب الزمن المقطوع

قانون الحرارة النوعية نحتاج الحرارة للقيام بعملية تسخين أي شيء، لكن كمية الحرارة التي نحتاجها لتسخين أي شيء لا تكون موحدة لجميع الأشياء، ولهذا نحتاج معرفة الحرارة النوعية من أجل ذلك، ويتم تمثيل صيغة المعادلة للتعبير عن الحرارة المطلوبة لتغيير درجة حرارة الجسم على النحو الآتي: (الحرارة النوعية) = (التغير في الطاقة الحرارية) / (الكتلة) × (التغير في درجة الحرارة). بالرموز: (C = ΔQ / (m ΔT حيث إن كلاً من: الحرارة النوعية = C التغير في الطاقة الحرارية = ΔQ الكتلة = m التغير في درجة الحرارة = ΔT

قانون الكثافة تُعرف الكثافة على أنّها مقدار كتلة وحدة الحجم لأي جسم أو مادة، لذا فإن كثافة أي مادة هي العلاقة التي تربط بين الكتلة والحجم للمادة، ويتم حساب الكثافة بواسطة قسمة الكتلة على الحجم، وتقاس الكثافة بوحدة الغرام لكل سنتيمتر مكعب، أو الكيلو غرام لكل متر مكعب، وتُكتب العلاقة رياضيًا لحساب كثافة أي جسم كما يأتي: الكثافة= الكتلة\ الحجم. ويُكتب قانون الكثافة بالرموز كما يأتي: ث= ك\ح حيث إنّ: ث: الكثافة ك: كتلة الجسم بالغرام أو الكيلوغرام. ح: حجم الجسم بالسنتمتر المكعب أو المترالمكعب. ويتم