تعليم

قانون محيط المستطيل عند معرفة أبعاده يُعّرف محيط المستطيل (بالإنجليزية: Perimeter of Rectangle) على أنه مجموع أطوال أضلاعه الأربعة، لكن من المعروف أن شكل المستطيل يمتاز بتساوي طول كل ضلعين متقابلين فيه، وهذا يعني أن محيطه يساوي ضعفي مجموع طوله وعرضه، وهو ما تعبر عنه المعادلة الحسابية الآتية: محيط المستطيل = 2 × (الطول العرض) وبالرموز: ح = 2 (ط ع)، إذ إن: ح: محيط المستطيل. ط: الطول. ع: العرض. مثال على حساب محيط المستطيل عند معرفة أبعاده ما هو محيط المستطيل الذي طوله 76.2 سم وعرضه 15.24 سم؟

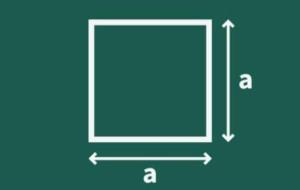
قانون محيط المربع يُمكن تعريف المربع (Square) على أنَّه شكل هندسي منتظم رُباعي الأضلاع ، جميع أضلاعه مُتساوية في الطول، وجميع زواياه متساوية أيضًا وهي زوايا قائمة قياس كل زاوية يساوي 90 درجة، ويُعرّف محيط المربع (Perimeter of a square) بأنّه المسافة الكلية للحدود الخارجية للمربع، وهو الطول الكلي لجميع جوانبه الأربعة، أي يُمكن إيجاد محيط المربع بجمع أطوال جميع أضلاعه ، ويُعبر عن محيطه بالصيغة الرياضية التالية: محيط المربع = 4 × طول الضلع. ويُمكن كتابة الصيغة الرياضية بالرموز على النحو التالي: ح

كيفية حساب محيط المربع يُمكن تعريف محيط المربع (Perimeter of a Square) بأنّه المسافة الكلية حول الحدود الخارجية للمربع، و يعد المربع أحد الأشكال الهندسية المستوية في الرياضيات ، لذا فإنّ جميع أطوال أضلاعه الأربعة متساوية في الطول، ويُمكن قياس محيط المربع باستخدام عدة قوانين وهي كالتالي: محيط المربع باستخدام طول الضلع وبما أنّ المحيط هو المسافة الكلية للحدود الخارجية أي أنّه مجموع جميع أطوال أضلاع المربع، ويُعبر عن قانون حساب محيط المربع باستخدام طول الضلع بالصيغة الرياضية التالية: محيط المربع

حساب محيط المثلث متساوي الساقين يمكن تعريف المثلث متساوي الساقين (بالإنجليزية: Isosceles Triangle) بأنّه المثلث الذي يتساوى فيه طول ضلعين، وزاويتين ، ويُمكن إيجاد محيط المثلث متساوي الساقين (بالإنجليزية: Isosceles Perimeter) وهو المسافة المحيطة به من الخارج إذا عُلم طول أحد ضلعيه وطول قاعدته باستخدام الصيغة الآتية: محيط المثلث متساوي الساقين= 2×طول الساق طول القاعدة، وبالرموز: ح=2×أ ب، حيث إنّ: أ: طول أحد الضلعين المتساويين، أو طول الساق. ب: طول قاعدة المثلث متساوي الساقين. حساب محيط المثلث

القانون العام لمحيط المثلث يُعرف المحيط على أنّه مجموع أطوال جميع جوانب المضلع أو أيّ شكل آخر، ووحدة قياس المحيط هي نفس وحدة القياس المستخدمة لقياس المسافة الخطية لأحد جوانب الشكل، ويتم حساب محيط المثلثات باتباع القانون الآتي: محيط المثلث= أ ب ج حيث إنّ: أ= طول الضلع الأول. ب= طول الضلع الثاني. ج= طول الضلع الثالث. أمثلة على حساب محيط المثلث باستخدام القانون العام مثال: مثلث طول ضلعه الأول 203سم والثاني 208سم والثالث 145سم، جد محيطه. الحل: بتعويض قيم الأضلاع المعطاة في قانون محيط المثلث

قانون محيط الدائرة يُمكن حِساب محيط الدائرة من خلال أحد القوانين الآتية : محيط الدائرة= قُطر الدائرة×π وبالرموز: ح=ق×π محيط الدائرة= 2×نصف قُطر الدائرة×π وبالرموز: ح=2×نق×π محيط الدائرة= الجذر التربيعي للقيمة (4×مساحة الدائرة×π) وبالرموز: ح= (4×م×π)√ حيث أن: م: مساحة الدائرة . ح: محيط الدائرة. نق: نصف قطر الدائرة، وهو المسافة الواصلة بين المركز وأية نقطة على محيط الدائرة. ق: طول قطر الدائرة، وهو يعادل المسافة الواصلة بين أية نقطتين على محيط الدائرة عند مرورها في المركز. π: الثابت باي، وتساوي

قانون حساب طول أقطار متوازي الأضلاع يمكن تعريف قطري متوازي الأضلاع بأنّهما الخطان المستقيمان الواصلان بين كل زاويتين متقابلتين فيه، أما عن طولهما فيمكن قياسه باستخدام القانون الآتي: طول القطر (ق،ل) = الجذر التربيعي (أ ب -2×أ×ب×جتا(أَ)). أما القانون الذي يربط بين طول أضلاع متوازي الأضلاع، وبين طول أقطاره فهو كالآتي: ق ل =2×(أ ب ) إذ إن: ق: طول القطر الأول. ل: طول القطر الثاني. أ: طول الضلع الأول لمتوازي الأضلاع. ب: طول الضلع الثاني لمتوازي الأضلاع. أَ: الزاوية المحصورة بين الضلعين أ، ب،

نص قانون لينز للحث الكهرومغناطيسي ينص قانون لينز للحث الكهرومغناطيسي على أنّ اتجاه التيار المُستحث في الموصل بواسطة مجال مغناطيسي مُتغيّر، وقد سُمّي قانون لينز بهذا الاسم نسبةً للعالم الفيزيائي إميل لينز، ويعتمد القانونعلى مبدأ حفظ الطاقة وقانون نيوتن الثالث، ويُمكن استخدامه لتحديد اتجاه التيار المُستحث أو القوة الدافعة الكهربائية (emf)، وهذا التيار المستحث ينتج وفقًا للمجال المغناطيسي المتغير خلال ملف من الأسلاك وذلك وفقًا لقانون فارادي، إذ يتدفّق هذا التيار في موصل خارجي بحيث يولّد مجالًا

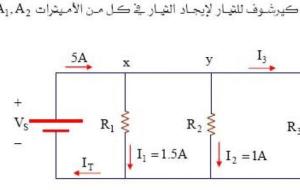
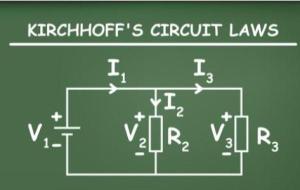
نص قانون كيرشوف للتيار ينص قانون كيرشوف للتيار (بالإنجليزية: Kirchhoff's current law) على أنّ قيمة التيار أو الشحنة الكهربائية التي تدخل إلى عقدةٍ معينة في الدارة تساوي قيمة التيار الذي يخرج منها، وبكلماتٍ أخرى فإن ذلك يعني أن مجموع التيارات الجبرية في أي نقطة تفرع يساوي صفراً، أو أن مجموع التيارات الجبرية الداخلة إلى عقدةٍ معينة، تعادل مجموع التيارات الجبرية الخارجة منها، ويتم التعبير عنه رياضياً من خلال القانون الآتي: التيار الداخل إلى العقدة (C) =مجموع التيارات الخارجة (c1 c2 c3 ....) فإذا

نص قانون كيرشوف الأول للتيار يسمى قانون كيرشف الاول (بالإنجليزية: Kirchhoff's Current Law) بقانون التيار، والذي يعمل على مبدأ حفظ الشحنة، إذ إن القانون ينص على أنه "عند أي نقطة في الدارة الكهربائية فإن مجموع جميع التيارات يكون مساويًا للصفر". مع الأخذ بعين الاعتبار اتجاه حركة التيار، والانتباه إذا كان التيار داخل إلى هذه النقطة أم خارج منها؛ فإن التيار إذا كان داخلًا في النقطة يعتبر موجبًا، وأما إذا كان خارجًا من النقطة يعتبر سالبًا. تعد قوانين كيرشوف من القوانين المهمة في علم الفيزياء ،

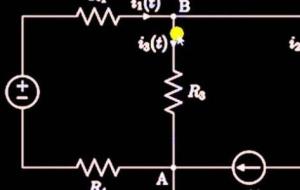
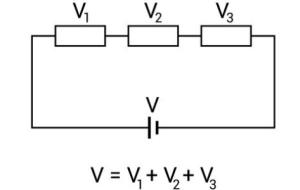
نص قانون كيرشوف الثاني ينص قانون كيرشوف الثاني أو قانون الجهد (بالإنجليزية: Kirchhoff Volt Law) على أنّ المجموع الجبري للتغيَّر في الجهد الكهربائي عبرمكوّنات أي حلقة كهربائية مُغلقة يساوي صفراً وهذا لعدم وجود أي شكل من أشكال ضياع الطاقة عبر المسار المُغلق اعتماداً على مبدأ حفظ الطاقة . فعندما تُحرّك القوة الدافعة الكهربائية التيار عبر مكونات الدائرة الكهربائية المغلقة كالمقاومات والخلايا الكهربائية، فإنّ ذلك قد يؤدي إلى فقدان أواكتساب للطاقة اعتماداً على نوع المكوّن وشدّة التيار في الدائرة

قانون كيرشوف الأول للتيار اكتشف عالم الفيزياء الألماني جوستاف روبرت كيرشوف (بالإنجليزية: Gustav Robert Kirchhoff) قوانين كيرشوف التي تسمح بحساب التيارات وشدّتها ومقاومات الشبكات الكهربائية، والتي أعلن عنها لأول مرّة في عام 1845م. وفيما يأتي تفسير لقانون كيرشوف الأول للتيار: نص قانون كيرشوف الأول وشرحه ينصّ قانون كيرشوف الأول للتيار (بالإنجليزية: Kirchhoff's Current Law) على أنّ التيار المتدفّق إلى عقدة أو تقاطع أسلاك في دارة يجب أن يكون مساويًا للتيار الخارج من ذلك التقاطع، ويكون ذلك نتيجةً

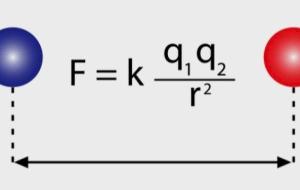
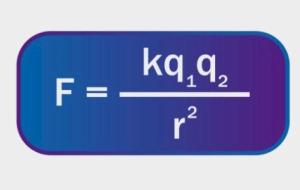
التعريف بقانون كولوم يعرّف قانون كولوم (Coulomb’s Law) بأنّه القانون الذي يحسب القوّة الكهربائيّة التي تؤثّر بها الشحنات الكهربائيّة على بعضها، ويُنسب اكتشاف القانون لعالم الفيزياء الفرنسي شارل أوغستان دي كولوم في نهايات القرن الثامن عشر والذي سمّي القانون باسمه فيما بعد. استعان كولوم بجهاز يسمّى بميزان اللّي (Torsion Balance) للوصول إلى هذا القانون، ووجد تجريبيًا تكوّن قوّة كهربائيّة بين الجسميات المشحونة; حيث أنّ الجسيمات ذات الشحنات المتشابهة تنشأ بينها قوى تنافر، أمّا الجسيمات ذات الشحنات

شرح مبسط لقانون كولوم يشرح قانون كولوم تأثير الشحنات الكهربائيّة على بعضها ومقدار القّوة الناتجة عن هذا التأثير، إذ تنشأ قوىً كهربائيّة متبادلة بين الشحنات، فالشحنات الكهربائيّة المختلفة تتجاذب والشحنات المتشابهة تتنافر، ويعبَّر عن مقدار قوى التجاذب والتنافر باستخدام قانون كولوم الذي وضعه العالم الفرنسي كولوم. نص قانون كولوم ينصّ قانون كولوم على أنّ القوة الكهربائيّة المتبادلة - تنافر أو تجاذب ـ بين شحنتين تفصل بينهما مسافة محددّة تتناسب طردياً مع مقدار كلا الشحنتين، وعكسياً مع مربع المسافة

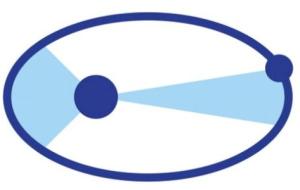
نص قانون كبلر الثاني يَنص القانون على الآتي: عند رسم خطوط وهمية بين مركز الشمس والكوكب الذي يَدور حولها على فترات زمنية محددة ومتساوية، فإن تلك الخطوط سوف تُشكّل مساحات متساوية فيما بينها، بغض النظر عن بعدهما عن بعضهما البعض، يُعرف قانون كبلر الثاني (بالإنجليزيّة: Kepler's Second Law) أيضًا باسم قانون المساحات المتساوية (بالإنجليزيّة: The Law of Equal Area). يدرس قانون كبلر الثاني تأثير عاملين رئيسين على العلاقة التي تربط بين كوكب ما والشمس، وهما كالآتي: المسافة كلما قلّت المسافة الفاصلة بين

نص قوانين فاراداي في التحليل الكهربائي قوانين فاراداي في التحليل الكهربائي هي قوانين كمية اكتشفها العالم الإنجليزي مايكل فاراداي في عام 1833 بعد دراسته للتحليل الكهربائي، وتوصل إلى قانونين يُعبران عن التغيرات الكيميائية وعلاقتها مع كمية التيار المُستخدم أثناء عملية التحليل الكهربائي، وفيما يلي توضيح مفصل لقوانين فارادي: القانون الأول في التحليل الكهربائي يُمكن تعريف قانون فاراداي الأول بأنّه كمية الترسب الكيميائي عند الأقطاب الناتجة من تدفق التيار الكهربائي تتناسب طرديًّا مع كمية الكهرباء التي

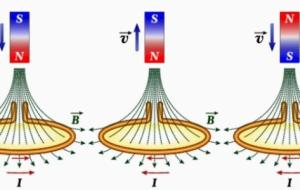
نص قانون فاراداي ينص قانون فارادي على أن التغيرات الحاصلة في معدل التدفق المغناطيسي للملف يمكن أن تولد قوة دافعة كهربائية، والتي بدورها تولد تياراً كهربائياً متناوباً. يصف قانون فارادي العلاقة بين معدل تغير تدفق المجال المغناطيسي Δϕ وحجم القوة الدافعة الكهربائية ε، إذ يتناسب معدل التغير في التدفق المغناطيسي طرديًا مع معدل التغير في الزمن، وعكسيًا مع القوة الدافعة الكهربائية. اكتشف الفيزيائي الإنجليزي مايكل فارادي العلاقة بين تدفق المجال المغناطيسي والقوة الدافعة الكهربائية في القرن التاسع عشر

طريقة حساب طول قوس الدائرة فيما يأتي الصيغ الرياضية المستخدمة لقياس طول قوس الدائرة وهي: عندما تُعطى الزاوية بالراديان يمكن استخدام الصيغة الآتية: طول القوس= نق×θ حيث أن: نق: نصف قطر الدائرة، وهو المسافة من مركزها إلى محيطها. θ: الزاوية المركزية المقابلة للقوس ومقاسة بالراديان، ويجدر بالذكر هنا أن: 360 درجة= 2πراديان. π: الثابت باي، وقيمته تساوي 3.14. عندما تُعطى الزاوية بالدرجات يمكن استخدام الصيغة الآتية: طول القوس= (2×π×نق×θ) / 360 حيث أن: نق: نصف قطر الدائرة، وهو المسافة من مركزها إلى

ما هي طاقة الوضع المرونية؟ طاقة الوضع المرونية (بالإنجليزية: Elastic potential energy) هي الطاقة المخزنة في الأجسام عند دفعها أو سحبها أو الضغط عليها، وتعبر طاقة الوضع المرونية عن الطاقة المخزنة في جسم ما بسبب موقعه بالنسبة إلى موضع مرجعي كسطح الأرض مثلاً وتعرضه للسحب أو الضغط كما في الزنبرك. ما هي وحدة طاقة الوضع المرونية؟ تقاس طاقة الوضع المرونية بالجول (بالإنجليزية: joules J) وهي إحدى وحدات النظام العالمي، تنسب إلى العالم للعالم الفيزيائي جيمس بريسكوت جول (بالإنجليزية: James Prescott

صيغ قانون ضعف الزاوية يرتبط مفهوم قانون ضعف الزاوية (بالإنجليزية: Double Angle) بالاقترانات المثلثية الثلاث، وهي الجيب، وجيب التمام، والظل، والتي هي عبارة عن علاقات تربط بين أضلاع المثلث قائم الزاوية بالنسبة لزواياه، ويجدر بالذكر أنّ ضعف الزاوية يعني ضرب قياس الزاوية بالعدد 2، أو مضاعفته، ولقانون ضعف الزاوية أشكال عدة هي: جا (2س)=2 جا(س) جتا(س)=2 ظا(س)/ (1 ظا²(س)). جتا (2س)=جتا²(س)-جا²(س)=2 جتا²(س)-1=1-2 جا²(س)=(1-ظا²(س))/(1 ظا²(س)). ظا (2س)=2 ظا(س)/ (1-ظا²(س)). أمثلة تطبيقية على قانون ضعف

قانون شدة المجال الكهربائيّ تُعرّف شدّة المجال الكهربائيّ (Electric Field Intensity) بأنّها القوة الكهربائيّة الناتجة من شحنة كهربائيّة، وهي كميّة متجهة لها مقدار واتجاه، كما أنّ وحدة قياس شدّة المجال الكهربائيّ تيوتن / كولوم. ويُمكن حساب شدّة المجال الكهربائيّ باستخدام القوانين الآتية: قانون شدّة المجال الكهربائيّ بالنسبة لشحنة الاختبار تُعرف شدّة المجال الكهربائيّ بأنّها القوة الكهربائيّة لكلّ شحنة اختبار، ويُمكن تمثيل هذه العلاقة بالقانون الآتي: شدة المجال الكهربائيّ = القوة الكهربائيّة /

قانون شحن البطارية فيما يأتي شرح لقوانين حساب شحن البطارية؛ زمن الشحن، وزمن التفريغ، وقانون عمر البطارية أيضًا: قانون حساب زمن شحن البطارية في البداية لا بدّ من التنويه إلى أنّ لكل جهاز كهربائيّ، مثل البطارية، قوانين فيزيائيّة تُستخدم لحساب القدرة الكهربائيّة ، والتيّار، والزمن وغيرها، وفيما يلي قانون حساب زمن شحن البطارية: T = AH / A، بحيث تُشير الرّموز المذكورة في القانون إلى ما يلي: T: زمن شحن البطاريّة بالسّاعات. AH: سعة البطاريّة أو السّعة الأمبيريّة للبطاريّة في السّاعة. A: التيّار

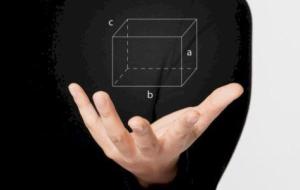
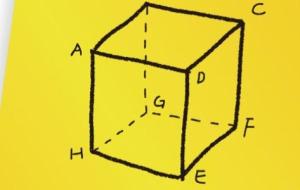
قوانين شبه المكعب شبه المكعب هو عبارة عن متوازي المستطيلات الذي يُعتبر إحدى المجسمات الثلاثية الأبعاد، وقائمة الزوايا، وأبعاده الثلاثة هي: الطول، والعرض، والارتفاع، ويتكون شبه المكعب من ستة أوجه مستطيلة الشكل، كل وجهين منها متطابقان، وتتلاقى هذه الوجوه عند الأحرف، التي هي عبارة عن خطوط مستقيمة تلتقي كل ثلاثة منها في نقاط تُعرف باسم الرؤوس، ويختلف عن المكعب من ناحية أن وجوهه مستطيلة وليست متطابقة، كما أن أبعاده مختلفة وغير متساوية. قانون مساحة شبه المكعب يُعدّ شبه المكعب مُجسّماً متعدد الأوجه،

قانون شارل يدرس قانون شارل العلاقة بين درجة الحرارة والحجم، حيث درس العالم جاكوس شارلز مدى تأثير درجة الحرارة على حجم الغاز، وتوصل إلى أنه عند ثبوت ضغط نوع من الغازات، فإن التناسب بين حجمه ودرجة حرارته يكون طردياً، أي أنّ درجة الحرارة تزداد بزيادة حجم الغازعند ثبات الضغط، والعكس صحيح. وُجد أن التمثيل الهندسي لقانون شارل هو رسم خط مستقيم، بحيث يتقاطع هذا الخط مع المحور الصادي (محور الحجم) أي أنّ درجة الحرارة تساوي -٢٧٣٫١٥ º م عندما يكون الحجم صفراً، وفي عام 1848م أجرى العالم كلفن دراسات أثبتت