قانون كبلر الثاني

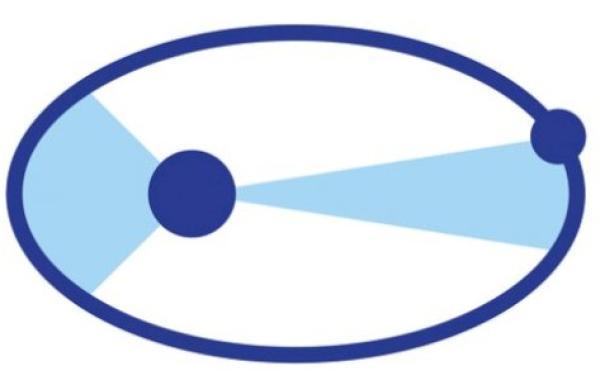
نص قانون كبلر الثاني

يَنص القانون على الآتي: عند رسم خطوط وهمية بين مركز الشمس والكوكب الذي يَدور حولها على فترات زمنية محددة ومتساوية، فإن تلك الخطوط سوف تُشكّل مساحات متساوية فيما بينها، بغض النظر عن بعدهما عن بعضهما البعض، يُعرف قانون كبلر الثاني (بالإنجليزيّة: Kepler's Second Law) أيضًا باسم قانون المساحات المتساوية (بالإنجليزيّة: The Law of Equal Area).

يدرس قانون كبلر الثاني تأثير عاملين رئيسين على العلاقة التي تربط بين كوكب ما والشمس، وهما كالآتي:

• المسافة

كلما قلّت المسافة الفاصلة بين كوكب ما والشمس زادت سرعة دورانه، والعكس صحيح، فالعلاقة بينهما طردية.

• السرعة

تتغير السرعة التي يدور بها كوكب ما حول الشمس باستمرار، وهذا يؤثر على المساحات المُغطّاة الناتجة عن دوران الكوكب على فترات من الزمن، ويُمكن تمثيلها عن طريق رسم مثلثات وهمية بخط يصل بين مركز الشمس ومركز الكوكب وقياس مساحاتها بين كل حركة وأخرى.

معادلة قانون كبلر الثاني

يساعد قانون كبلر الثاني في حساب المساحة المُغطاة بين مركز الشمس والكوكب الذي يدور حولها، بمعنى آخر مقدار السرعة المساحية نسبًة لمرور الوقت، وهو ما يُعبّر عنه بالصيغة الرياضية الآتية:

(Areal Velocity = Angular Momentum / (2 × Mass of the Planet

وبالرموز:

(Areal Velocity = ΔA / Δt = L / (2 × m

حيث إنّ:

• ΔA/Δt: السرعة المساحية بوحدة م/ث.
• L: الزخم الزاوي بوحدة كغ.م²/ث.
• m: كتلة الكوكب بوحدة كغ.

السرعة المساحية = الزخم الزاوي / (2 × كتلة الكوكب)

وبالرموز:

س _م = خ _ز / (2 × ك)

حيث إنّ:

• س _م: السرعة المساحية بوحدة م/ث.
• خ _ز: الزخم الزاوي بوحدة كغ.م²/ث.
• ك: كتلة الكوكب بوحدة كغ.

من الجدير بالذكر أن معدل السرعة المساحية أو معدل تغير المساحة مع مرور الوقت ثابت للكوكب الواحد، لأن الزخم الزاوي محفوظ كميًا .

اشتقاق قانون كبلر الثاني

يُشّتق قانون كبلر الثاني بالاعتماد على العلاقة التي تربط بُعد الكوكب عن الشمس بالسرعة المساحية، على النحو الآتي:

• رسم خط وهمي يربط بين مركزي الكوكب والشمس، على أن يكون مقدار المسافة الفاصلة بينهما r، ويتشكّل مثلث من ذلك الخط زاويته φ وارتفاعه المتمثل بحركة الكوكب تساوي r dφ.
• تطبيق قانون مساحة المثلث، عندها سينتج الآتي:

مساحة المثلث = ½ × القاعدة × الارتفاع

ومنه:

dA = ½ × r × r(dφ)

• حساب المساحة عن طريق قسمة طرفي المعادلة على الوقت، كالآتي:

dA/dt = ½ × r × (rdφ / dt)

• تعويض قيمة السرعة الزاوية في (r dφ / dt )، ليُصبح القانون على النحو الآتي:

dA/dt = ½ × r × vφ

• تعويض قيمة الزخم الزاوي الذي يُعبّر عنه كما يأتي:

Angular Momentum of the Planet = Mass × Distance × Velocity الزخم الزاوي = كتلة الكوكب × بُعد الكوكب × السرعة التي يدور بها الكوكب

• كتابة الصيغة النهائية لقانون كبلر الثاني على النحو الآتي:

(Areal Velocity = Angular Momentum / (2 × Mass of the Planet

السرعة المساحية = الزخم الزاوي / (2 × كتلة الكوكب)

يختص قانون كبلر الثاني بدراسة العلاقة التي تربط بين بعد كوكب ما عن الشمس وسرعة دورانه، ذلك أن سرعة الكوكب تتغير بشكل مستمر مع الزمن، ويُمكن حساب السرعة المساحية لحركة الكوكب بالاعتماد على قانون كبلر الثاني، والذي يساوي نصف مقدار الزخم الزاوي للكوكب مقسومًا على كتلته.