قانون كولوم
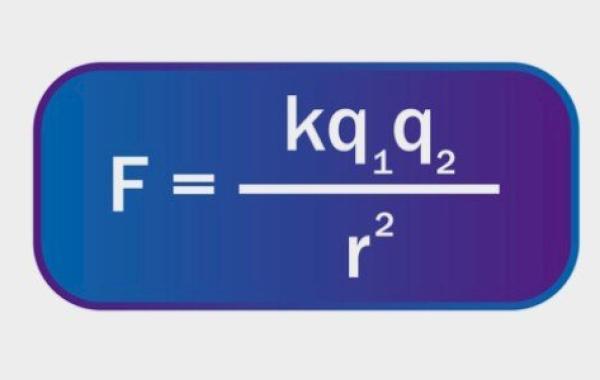
شرح مبسط لقانون كولوم
يشرح قانون كولوم تأثير الشحنات الكهربائيّة على بعضها ومقدار القّوة الناتجة عن هذا التأثير، إذ تنشأ قوىً كهربائيّة متبادلة بين الشحنات، فالشحنات الكهربائيّة المختلفة تتجاذب والشحنات المتشابهة تتنافر، ويعبَّر عن مقدار قوى التجاذب والتنافر باستخدام قانون كولوم الذي وضعه العالم الفرنسي كولوم.
نص قانون كولوم
ينصّ قانون كولوم على أنّ القوة الكهربائيّة المتبادلة - تنافر أو تجاذب ـ بين شحنتين تفصل بينهما مسافة محددّة تتناسب طردياً مع مقدار كلا الشحنتين، وعكسياً مع مربع المسافة الفاصلة بينهما.
الصيغة الرياضية لقانون كولوم
يمكن التعبير عن قانون كولوم رياضيًا كالآتي:
ق = أ (شـ1 شـ2) / ف²، وتعبّر كل من هذه الرموز عن:
- ق: هي القوة الكهربائية المتبادلة ووحدتها نيوتن.
- أ: هو ثابت التناسب ويساوي 8.9875×10 ⁹ ولغرض الحسابات فإنّها تقّرب إلى 9×10 ⁹ ووحدته هي نيوتن.م²/ كولوم².
- شـ1 شـ2: هي مقدار كل من الشحنة الأولى والشحنة الثانية، ووحدتها الكولوم.
- ف: هي المسافة بين كل من الشحنتين، ووحدتها المتر.
أمثلة وتطبيقات على قانون كولوم
تاليًا أمثلة على قانون كولوم.
لإيجاد مقدرة القوة المؤثرة عندما يكون مقدار الشحنتين معلومًا
إذا علمت أنّ شـ1 = 1 × 10 كولوم، شـ2 = -25 × 10 ، يفصل بينهما مسافة 50 سم، ما مقدار القوّة المؤثّرة في الشحنة الأولى والشحنة الثانية، ماذا يُلاحَظ؟ وما نوع القوّة بينهما؟
الحل:
القوّة المؤثّرة في الشحنة الأولى:
ق = أ (شـ1 شـ2 ) / ف ²
- ق = 9×10 ⁹ (1 × 10 ) ( 25 × 10 ) / (50 × 10 ) ²
- ق = 900 نيوتن.
القوّة المؤثّرة في الشحنة الثانية:
- ق = أ (شـ2 شـ1) / ف ²
- ق = 9×10 ⁹ (25 × 10 ⁵ ) (1 × 10 ⁴ ) / (50 × 10 ) ²
- ق = 900 نيوتن.
يُلاحَظ أنّ مقدار القوّتين متساوي، أي أنّ القوّة التي تؤثّر بها الشحنة الأولى على الثانية تساوي القوّة التي تؤثّر بها الشحنة الثانية على الأولى، ونوع القّوة المتبادلة بينهما هي قوى تجاذب لأنّ الشحنتين مختلفتين نوعاً.
عندما تكون قيمة الشحنتين مجهولة
شحنتان موجبتان إحداهما أربع أمثال الشحنة الأخرى والبعد بينهما 6 م، ما مقدارهما إذا عُلم أنّ القوّة المتبادلة بينهما تساوي 0.9 نيوتن:
الحلّ:
- نفرض ش1 = ش، ومنه ش2 = 4 ش.
- ق = أ (شـ1 شـ2 ) / ف ²
- ق = 9×10 ⁹ (شـ × 4 شـ ) / ف ²
- 0.9 = 9×10 ⁹ ش² / ( 6) ²
- شـ = ± (3 × 10 ) كولوم وهي قيمة الشحنة الأولى، ويرفض الجذر السالب لأنّ الشحنتين موجبتين من معطيات السؤال.
- ولأنّ الشحنة الثانية تساوي 4 أضعاف الشحنة الثانية فإنّ:
- ش2 = 4 (3 × 10 ) = 12 × 10 كولوم.
إيجاد مقدار القوة المتبادلة من قوة كهربائية سابقة معلومة
شحنتان تتبادلان قوّة كهربائيّة مقدارها 90 نيوتن، كم يصبح مقدار القوّة الكهربائيّة المتبادلة إذا أصبحت القوّة المتبادلة بينهما كما يأتي:
- 3 أمثال ما كانت عليه.
- نصف ما كانت عليه.
الحلّ:
- ق1 = 9×10 ⁹ (شـ1 شـ2 ) / ف ²
- 90 = 9×10⁹ (شـ1 شـ2) / ف²
إذا أصبحت القوّة المتبادلة بينهما 3 أمثال ما كانت عليه:
- ف = 3 ف
- ق2 = 9×10⁹ (شـ1 شـ2) / (3 ف)².
- ق2 = 9×10⁹ (شـ1 شـ2) / 9 (ف)².
- لكنّ ق1 = 9×10 ⁹ (شـ1 شـ2 ) / ف ² وتساوي 90 نيوتن كما ورد في معطيات السؤال، فيُلاحظ أنّ تعويض المسافة الجديدة في القانون تجعل قيمة ق2 تساوي ق1 مقسومًا على 9 كالآتي:
- ق2 = 1/9 ق1.
- ق2 = 1/9 × 90 = 10 نيوتن.
إذا أصبحت القوّة المتبادلة بينهما نصف ما كانت عليه:
- ف = 1/2 ف
- ق2 = 9×10⁹ (شـ1 شـ2) / (1/2 ف)².
- ق2 = 9×10⁹ (شـ1 شـ2) / 1/4 (ف)²، وبعد التبسيط يكون شكل المعادلة كالآتي:
- ق2 = (4) (9×10⁹) (شـ1 شـ2) / (ف)².
- لكنّ ق1 = 9×10 ⁹ (شـ1 شـ2 ) / ف ² وتساوي 90 نيوتن كما ورد في معطيات السؤال، فيُلاحظ أنّ تعويض المسافة الجديدة في القانون تجعل قيمة ق2 تساوي 4 أضعاف ق1 كالآتي:
- ق2 = 4 ق1.
- ق2 = 4 × 90 = 360 نيوتن.
شرح متخصص لقانون كولوم
يطَبّق قانون كولوم على الشحنات الكهربائيّة النقطيّة أو الأجسام الكرويّة المشحونة والتي تتمركز شحنتها في مركزها، وتوصف القوّة الكهربائيّة بين الشحنات على أنّها متبادلة لأنّ الشحنة الأولى عندما تؤثّر على الشحنة الثانية بقوّة فعل، فإنّ الشحنة الثانية تؤثّر على الشحنة الأولى بقوّة ردّ فعل مساوية في المقدار ومعاكسة في الاتجاه لقوّة الفعل، وذلك حسب قانون نيوتن الثالث.
تتأثّر القوّة الكهربائيّة المتبادلة بين الشحنات بعدّة عوامل يمكن استنتاجها من خلال قانون كولوم، وهذه العوامل كما يأتي:
- سماحيّة الوسط الكهربائي، ورمزها (ε)، وعلاقتها عكسيّة مع مقدار القوّة الكهربائيّة، ومن خلال تحديد هذه القيمة يمكن حساب ثابت التناسب (أ) حيث أنّ قيمة الثابت أ = ، وفي حال كان الوسط الفاصل بين الشحنات هو الهواء فإنّ ثابت التناسب يساوي 8.9875×10⁹.
- مقدار كل من الشحنتين الكهربائيتين (ش1 ش2) يتناسب طرديًا مع مقدار القوّة الكهربائيّة.
- مربّع المسافة الفاصلة بين الشحنتين (ف²) يتناسب عكسيًا مع مقدار القوة الكهربائية، ولذلك فإنّ قانون كولوم يسمّى أيضاً بقانون التربيع العكسي.
الصيغة العددية
يمكن التعبير عن قانون كولوم بصيغة علميّة دقيقة بالصورة الآتية:
ق = 1/(4πε) × (ش1 ش2) / ف²
الصيغة المتجهية
يعطي قانون كولوم مقدار القوّة الكهربائيّة فقط، لكنّ القوة كميّة متجهة، لذلك لا بدّ من وصفها اتجاهًا أيضًا، ويكون اتجاه القوّة الكهربائيّة دائمًا منطبقاً على الخطّ الواصل بين الشحنتين إذا كانت القوّة المتبادلة قوة تجاذب، في حين يكون اتجاهها على امتداد الخطّ الواصل بين الشحنتين إذا كانت القوّة تمثّل قوّة تنافر.
وحسب قانون نيوتن الثالث فإنّ هاتين القوتين متساويتين مقداراً ومتعاكستين اتجاهًا، لذا فإنّهما تمثّلان زوجًا من القوى المتبادلة كما يأتي:
ق 12 = - ق12، وتدلّ الإشارة السالبة على عكس الاتجاه.
ملخص المقال
يستخدم قانون كولوم بهدف حساب القوّة الكهربائيّة المتبادلة بين شحنتين كهربائيتين تفصل بينهما مسافة محددة، ويعتمد مقدار هذه القّوة على الوسط الفاصل بين الشحنتين، ومقدار كلّ من الشحنتين، ومقدار المسافة الفاصلة بينهما، وتُعرف القوة الكهربائيّة بين الشحنات بأنّها قوىً متبادلة أي أنّ كل من الشحنات لها تأثير مساوٍ لتأثير الشحنة الأخرى عليها، إلّا أنّ اتجاه التأثير متعاكس.