قانون نصف القطر
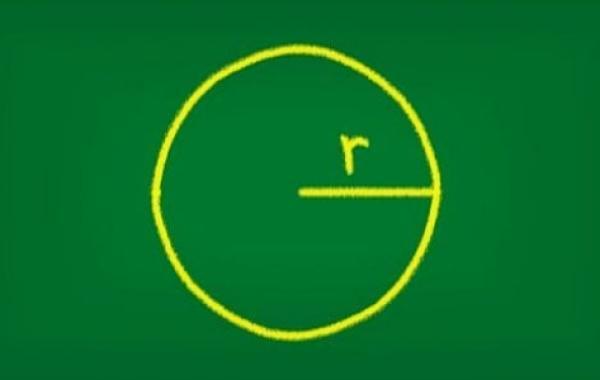
كيفية حساب نصف قطر الدائرة
يُعرّف نصف القطر الدائرة (بالإنجليزيّة: Radius of Circle) بأنّه الخط المستقيم الواصل بين مركز الدائرة ونقطة تقع على محيطها، ويُمكن حسابه بعدّة طرق وفقًا للمعطيات المتوفرة، وهي كالآتي:
حساب نصف القطر من محيط الدائرة
يُمكن حساب نصف القطر للدائرة عندما يكون محيطها معلومًا عن طريق الآتي:
- كتابة قانون محيط الدائرة :
محيط الدائرة = 2 × π × نصف القطر
- إعادة ترتيب قانون المحيط وجعل نصف القطر موضوع القانون ينتج الآتي:
نصف القطر = المحيط / 2 × π
وبالرموز:
نق = ح / 2 × π
حيث إنّ:
- نق: نصف قطر الدائرة بوحدة سم.
- ح: محيط الدائرة بوحدة سم.
- π: ثابت عددي قيمته التقريبية تساوي 3.14 أو 22/7.
حساب نصف القطر من مساحة الدائرة
يُمكن حساب نصف القطر للدائرة عندما تكون مساحتها معلومة عن طريق الآتي:
- كتابة قانون مساحة الدائرة :
مساحة الدائرة = π × نصف القطر²
- إعادة ترتيب قانون المساحة وجعل نصف القطر موضوع القانون ينتج الآتي:
نصف القطر = الجذر التربيعي لـ (المسافة/ π)
وبالرموز:
نق = (م / π)√
حيث إنّ:
- نق: نصف قطر الدائرة بوحدة سم.
- م: مساحة الدائرة بوحدة سم².
- π: ثابت عددي قيمته التقريبية تساوي 3.14 أو 22/7.
حساب نصف القطر من ثلاث نقاط على الدائرة
يُمكن حساب نصف القطر إذا عُلمت إحداثيات 3 نقاط تمر خلالهم الدائرة، عن طريق الآتي:
- كتابة معادلة الدائرة العامة:
س² ص² (2 × أ× س) (2 × ب × ص) جـ = 0
حيث إنّ:
- س، ص: إحداثيات كل نقطة من النقاط الثلاثة التي تمر عبرهم الدائرة.
- أ، ب: إحداثيات مركز الدائرة.
- جـ: ثابت.
فإذا مرّت الدائرة بالنقاط: (س1،ص1)، (س2،ص2)، (س3،ص3)، وبتعويض قيمهم في معادلة الدائرة العامة نحصل على الآتي:
- (س1)² (ص1)² (2 × أ × س1) (2 × ب × ص1) جـ = 0
- (س2)² (ص2)² (2 × أ × س2) (2 × ب × ص2) جـ = 0
- (س3)² (ص3)² (2 × أ × س3) (2 × ب × ص3) جـ = 0
تُعوض قيم الإحداثيات في المعادلات أعلاه لإيجاد قيم (أ، ب، جـ).
تُعوض إحداثيات مركز الدائرة (أ، ب) وقيمة جـ في قانون نصف القطر وهو كالتالي:
نق = (أ² ب²-جـ)√
كيفية حساب نصف قطر الكرة
يُعرّف نصف قطر الكرة (بالإنجليزيّة: Radius of a Sphere) بأنّه الخط المستقيم الواصل بين مركز الكرة وأي نقطة تقع على سطحها، ويُمكن حسابه بعدة طرق وفقًا للمعطيات المتوفرة، وهي كالآتي:
حساب نصف القطر من حجم الكرة
يُمكن حساب نصف القطر للكرة عندما يكون حجمها معلومًا عن طريق الآتي:
- كتابة قانون حجم الكرة:
محيط الكرة = ¾ × π × نصف القطر³
- إعادة ترتيب قانون الحجم وجعل نصف القطر موضوع القانون ينتج الآتي:
نصف القطر = [(π × 4) / (3 × حجم الكرة)] √³
وبالرموز:
نق = [(π × 4) / (3 × ح)] √³
حيث إنّ:
- نق: نصف قطر الكرة بوحدة سم.
- ح: حجم الكرة بوحدة سم³.
- π: هو ثابت عددي قيمته التقريبية تساوي 3.14 أو 22/7.
حساب نصف القطر من مساحة الكرة
يُمكن حساب نصف القطر للكرة عندما تكون مساحتها معلومة عن طريق الآتي:
- كتابة قانون مساحة الكرة :
مساحة الكرة = 4 × π × نصف القطر²
- إعادة ترتيب قانون المساحة وجعل نصف القطر موضوع القانون ينتج الآتي:
نصف القطر = (π × 4) / (مساحة الكرة) √
وبالرموز:
نق = (π × 4) / م √
حيث إنّ:
- نق: نصف قطر الكرة بوحدة سم.
- م: مساحة الكرة بوحدة سم².
- π: هو ثابت عددي قيمته التقريبية تساوي 3.14 أو 22/7.
كيفية حساب نصف قطر الأسطوانة
يُعرّف نصف قطر الأسطوانة (بالإنجليزيّة: Radius of Cylinder) بأنّه نصف قطر قاعدتي الأسطوانة اللتين تمثلا دائرتين متطابقتين، بحيث يصل نصف قطر كل قاعدة بين مركزها وبين النقاط الواقعة على محيطها، ويُمكن حسابه بعدة طرق وفقًا للمعطيات المتوفرة، وهي كالآتي:
حساب نصف القطر من حجم الأسطوانة
يُمكن حساب نصف القطر للأسطوانة عندما يكون حجمها معلومًا عن طريق الآتي:
- كتابة قانون حجم الأسطوانة:
حجم الأسطوانة = π × مربع نصف قطر القاعدة × الارتفاع
- إعادة ترتيب قانون الحجم وجعل نصف القطر موضوع القانون ينتج الآتي:
نصف قطر الأسطوانة = (حجم الأسطوانة / (π × ارتفاع الأسطوانة)) √
وبالرموز:
نق = (ح / (π × ع)) √
حيث إنّ:
- نق: نصف قطر قاعدة الأسطوانة بوحدة سم.
- ح: حجم الأسطوانة بوحدة سم³.
- ع: ارتفاع الأسطوانة بوحدة سم.
- π: هو ثابت عددي قيمته التقريبية تساوي 3.14 أو 22/7.
حساب نصف القطر من المساحة الجانبية للأسطوانة
يُمكن حساب نصف القطر للأسطوانة عندما تكون مساحتها الجانبية معلومة عن طريق الآتي:
مساحة الأسطوانة الجانبية = 2 × π × نصف قطر القاعدة × الارتفاع
- إعادة ترتيب قانون المساحة الجانبية للإسطوانة وجعل نصف القطر موضوع القانون لينتج الآتي:
نصف قطر الأسطوانة = المساحة الجانبية / (2 × π × الارتفاع)
وبالرموز:
نق = م / (2 × π ×ع)
حيث أنّ:
- نق: نصف قطر قاعدة الأسطوانة بوحدة سم.
- م: مساحة الأسطوانة الجانبية بوحدة سم².
- ع: ارتفاع الأسطوانة بوحدة سم.
- π: هو ثابت عددي قيمته التقريبية تساوي 3.14 أو 22/7.
أمثلة متنوعة على حساب نصف القطر
ندرج فيما يأتي أمثلة متنوعة على حساب نصف القطر:
حساب نصف القطر من محيط الدائرة
إذا كان محيط الدائرة يساوي 26 سم، جد نصف قطرها.
الحل:
- كتابة المعطيات:
محيط الدائرة = 26 سم
- كتابة القانون:
نق = ح / 2 × π
- تعويض المعطيات:
نق = ح / 2 × π
نق = 26 / 2 × 3.14
نق = 4.14 سم
حساب نصف القطر من مساحة الدائرة
احسب نصف قطر الدائرة إذا كانت مساحتها 66 سم².
الحل:
- كتابة المعطيات:
مساحة الدائرة = 66 سم²
- كتابة القانون:
نق = (م / π)√
- تعويض المعطيات:
نق = (م / π)√
نق = (66 / 3.14)√
نق = 4.58 سم
حساب نصف القطر من ثلاث نقاط على الدائرة
جد نصف قطر الدائرة التي تمر عبر النقاط الثلاثة التالية: (6-،1)، (2،1)، (5،2).
الحل:
- كتابة القانون:
س² ص² (2 × أ × س) (2 × ب × ص) جـ = 0
- تعويض كل نقطة من النقاط الثلاثة في معادلة الدائرة العامة كالآتي:
إحداثيات النقطة الأولى: (س1= 1، ص1= 6-):
²1 (6-)² (2 × أ × 1) (2 × ب × 6-) جـ = 0
1 36 2 أ - 12 ب جـ = 0
37 2 أ - 12 ب جـ = 0
2 أ - 12 ب جـ = 37-
إحداثيات النقطة الثانية: (س2= 2 ، ص2= 1):
²2 ²1 (2 × أ × 2) (2 × ب × 1) جـ = 0
5 4 أ 2 ب جـ = 0
4 أ 2 ب جـ = 5-
إحداثيات النقطة الثالثة: (س3= 5 ، ص3= 2):
²5 ²2 (2 × أ × 5) (2 × ب × 2) جـ = 0
29 10 أ 4 ب جـ = 0
10 أ 4 ب جـ = 29-
- طرح المعادلة الثانية من المعادلة الأولى:
4 أ 2 ب جـ = 5-
2 أ - 12 ب جـ = 37- (-)
ــــــــــــــــــــــــــــــــــــــ
2 أ 14 ب = 32
ترتيب المعادلة لإيجاد قيمة أ بدلالة ب كالآتي:
أ = 16 - 7ب
- طرح المعادلة الثالثة من المعادلة الثانية:
10 أ 4 ب جـ = 29-
4 أ 2 ب جـ = 5- (-)
ــــــــــــــــــــــــــــــــــــــ
6 أ 2 ب = 24-
بقسمة المعادلة على 2 تُصبح:
3 أ ب = 12-
- تعويض قيمة أ (أ = 16 - 7ب ) في المعادلة لإيجاد قيمة ب كالآتي:
3 أ ب = 12-
3 (16 - 7ب) ب = 12-
48 - 21 ب ب = 12-
ب = 3
- تعويض قيمة ب لإيجاد قيمة أ:
أ = 16 - 7ب
أ = 16 - 7 × 3
أ = 5-
- تعويض قيم أ وب في أي معادلة من معادلات النقاط لإيجاد قيمة جـ:
4 أ 2 ب جـ = 5-
4 × 5- 2 × 3 جـ = 5-
جـ = 9
- تعويض قيم أ، ب، جـ في قانون نصف القطر:
نق = (أ² ب² - جـ)√
نق = ((5-)² (3)² - 9)√
نق = (25 9 - 9)√
نق = 5
حساب نصف القطر من حجم الكرة
يبلغ حجم جسم كروي الشكل 500 سم³، جد نصف قطره.
الحل:
- كتابة المعطيات:
حجم الكرة = 500 سم³
- كتابة القانون:
نق = [(π × 4) / (3 × ح)] √³
- تعويض المعطيات:
نق = (3.14 × 4) / (3 × 500) √³
نق = (12.56) / (1500) √³
نق = 4.92 سم
حساب نصف القطر من مساحة الكرة
إذا كانت مساحة سطح الكرة 250 سم²، جد نصف قطرها.
الحل:
- كتابة المعطيات:
مساحة الكرة = 250 سم²
- كتابة القانون:
نق = (π×4) / م √
- تعويض المعطيات:
نق = (3.14 × 4) / 250 √
نق = 4.46 سم
حساب نصف القطر من حجم الأسطوانة
ما هو نصف قطر الأسطوانة التي يبلغ حجمها 546 سم³ وارتفاعها 10 سم.
الحل:
- كتابة المعطيات:
حجم الأسطوانة = 546 سم³
ارتفاع الأسطوانة = 10 سم
- كتابة القانون:
نق = (ح / (π × ع))√
- تعويض المعطيات:
نق = (546 / (3.14 × 10))√
نق = 4.16 سم
حساب نصف القطر من المساحة الجانبية للأسطوانة
إذا علمتَ أنّ المساحة الجانبية لخزان ماء أسطواني الشكل تساوي 350 سم²، وارتفاعه 12 سم جد نصف قطر الخزان.
الحل:
- كتابة المعطيات:
المساحة الجانبية = 350 سم²
ارتفاع الخزان = 12 سم
- كتابة القانون:
نق = م / (2 × π ×ع)
- تعويض المعطيات:
نق = 350 / (2 × 3.14 × 12)
نق = 4.64 سم
يُعرّف نصف القطر للشكل الهندسي بأنّه الخط الواصل بين مركز الشكل الهندسي والنقاط الموجودة على محيطه، ويُمكن إيجاد قيمته باستخدام صيغ نصف القطر المُشتقة من القوانين الأساسية للمعطيات المتوفرة، مثل مساحة الشكل الهندسي، أو محيطه، أو حجمه، أو من خلال إحداثيات النقاط الواقعة على محيطه.