تعليم

تجربة انتشار الضوء ينتشر الضوء انطلاقا من المنبع الضوئي في جميع الإتجاهات عبر أوساط مختلفة، أوساط انتشار الضوء، وتصنف الأوساط المادية حسب قدرة الضوء على النفاذ، وينتشر الضوء في الأوساط الشفافة بسرعة كبيرة، والهدف الرئيسي من تجربة انتشار الضوء هو تحقيق قانون انعكاس الضوء. الأدوات التي نحتاجها في تجربة انتشار الضوء هناك أدوات بسيطة تستخدم لتجربة انتشار الضوء كالتالي: مرآة مستوية. ورقة بيضاء. دبابيس. قلم رصاصي. منقلة. خطوات تجربة انتشار الضوء هناك خطوات بسيطة لانجاز تجربة انتشار الضوء كالتالي:

كيفية صناعة العطور كيميائياً تمرّ العطور بمراحل متعددة لتصل إلى شكلها النهائي، وفيما يأتي توضيح لذلك: المكونات المستخدمة يُوجد العديد من المواد المستخدمة في صناعة العُطر الكيميائي، ويُمكن أنّ تكون المواد المستخدمة في إنتاج العطور مستخلصةً ممّا يأتي: الفواكه. التوابل. الأوراق. الأعشاب. الأزهار، وتُعدّ المكوّن الرئيسي، وأهمّ مادة خام في تصنيع العطور. المنتجات الحيوانية، مثل العنبر المُستخرج من حيتان العنبر، والمسك المُستخرج من ذكور الغزلان. المواد الكيميائية الاصطناعية. استخراج المكونات يتكوّن

الرسوم المتحركة تُعرف الرسوم المتحرّكة (بالإنجليزيّة:Animation) بأنّها عملية صنع وهم الحركة، عن طريق العرض السريع لتسلسل معيّن من الصور أو الرسمات، ثنائيّة أو ثلاثيّة الأبعاد، والتي تختلف عن بعضها اختلافاً بسيطاً ثمّ يزداد تدريجيّاً، وعادةً ما يُضاف لها بعض الأصوات، والمؤثّرات الصوتيّة، والموسيقى الخلفيّة. وتُستخدم الرسوم المتحرّكة في وسائل الإعلام فهي تمتلك قوّة التأثير والتسويق، كما تُستخدم لصناعة الأفلام الترفيهيّة، وفي برامج المحاكاة التدريبيّة، وفي التجارب العلميّة التي تحتاج لتجربة قبل

تعريف حروف المد حروف المدّ كما أوردنا سابقًا تنقسم إلى ثلاثة حروف وهي كالآتي: الألف الواو الياء كيفية تمييز حروف المد حروف المدّ {الألف والواو والياء} وهي حروف أصلية، أيّ أنها من الحروف الأبجدية، لكلٍّ منها لفظها ومخرجها وصوتها ووصفٌ تفصيلي لكلّ حرف فيما يأتي: سُمّيت بحروف المدّ لأن القارئ يلجأ إلى الإطالة في لفظها وإشباع حركتها وزيادة المُدّة الزمنية الكافية لنطقها، فمثلًا نقول عامر ونادر في الألف الممدودة ، ونقول سوء ونزول في واو المدّ، ونيران والزّير في ياء المدّ. الألف هو أول الحروف

ما المقصود بتقدير الذات؟ تقدير الذات هو ما يشعر به الإنسان تجاه نفسه، أو ما هو رأي الشخص بنفسه، وفي أغلب الأحيان يكون تقدير الذات ناتجاً عن تجارب وأحداث مرّ بها الشخص بالأخص في طفولته، لكن هذا لا يعني أنه لا يمكنه تطوير احترامه وتقديره لذاته، ولا يخلو الأمر بأن يتعرّض الإنسان إلى شكوك تجاه نفسه من وقت إلى آخر، حيث أن انخفاض تقدير الذات من الممكن أن يجعل الشخص يشعر بانعدام الأمان من حوله، ومن الجدير بالذكر أنه إذا استمرّت هذه الحالة طويلاً فإنها من الممكن أن تؤدي إلى مشاكل نفسية وصحية. كيفية

كيفية دوران الأرض حول نفسها تدور الأرض حول محورها الوهمي يومياً منذ حوالي 4.6 مليار سنة، و يتسبّب دوران الأرض حول نفسها بظاهرة تعاقب الليل والنهار ، حيث تحتاج إلى 24 ساعة لإتمام الدورة الواحدة. ويُذكر أنّ سرعة دوران الأرض تكون في أعلى مستوياتها عند خط الاستواء، وتقل كلّما انحنى محيطها للأعلى أو الأسفل حتّى تصل إلى أقل مستوياتها عند القطبين الجنوبي والشمالي؛ لذلك تكون سرعة الأرض مرتفعةً نسبياً في المناطق التي تتوسط الأرض، مثل: أوروبا، واليابان، وبعض أجزاء الولايات المتحدة الأمريكية، حيث تقترب

حماية التراث تعاونت الدول العربيّة منذ عام 1947م على إحياء التراث العربي، وتنشيطه، والحفاظ عليه، كما استُخدمت الوسائل المُختلفة لنشره بين الناس قدر استطاعتها، وفي عام 1970م، أُنشئت المنظمة العربيّة للتربية والثقافة والعلوم، التي تُواصل حتّى اليوم عملها في الحفاظ على التراث العربي، من خلال مجموعةٍ من البرامج والمشاريع المُختلفة، إضافةً إلى المؤتمرات التي تبحث في شؤون التراث الثقافيّ والآثار. حماية التراث الثقافي والطبيعي اهتمت منظمات عالميّة عديدة بالتراث على المستوى العالمي، فقد شجعت منظمة

دور الأفراد في حماية البيئة من البلاستيك يعد البلاستيك من أخطر المواد وأكثرها تسببًا في دمار الحياة على سطح الأرض، ولا يُعد هذه الأمر مُفاجئًا نظرًا لكمية البلاستيك الهائلة التي يستعملها البشر، إذ يقدر أنه خلال 31 سنة سوف يحتوي المحيط على البلاستيك أكثر من احتوائه على الأسماك، فهناك نحو 513 مليون طن من البلاستيك ينتهي مسارها إلى المحيط، ومن أضرار البلاستيك على البيئة وعلى الحياة المائية أن الأحياء المائية يمكن أن تعلق به أو تبتلعه، إضافةً إلى ذلك فهو يحتاج إلى ألف سنة أكثر من أنواع القمامة

طريقة حل جداول الدوال لإيجاد المخرجات يعرف جدول الدوال (بالإنجليزية: Function table) بأنه جدول عمودي أو أفقي يعتمد على قاعدة معينة تُستخدم في حساب المخرجات، فيكون لكل مدخل نتيجة واحدة خاصة به فقط، كما تسمى هذه العلاقة الرياضية بالدالة، ويمكن إيجاد مخرجات جداول الدوال عند حل جدول الدوال بالاعتماد على مدخلاته وقاعدته باتّباع الخطوات الآتية: رسم جدول فارغ بصفّين، وتسمية الصف الأول بالمدخلات والثاني بالمخرجات ويمكن رسم الجدول بصورة عمودية أيضًا، كما يأتي: المدخلات المخرجات أو المدخلات المخرجات

خطوات لحل مسائل الرياضيات الصعبة تتنوع المسائل الرياضية في درجة صعوبتها، فمنها ما هو بسيط ومباشر، ومنها ما هو بحاجة إلى التركيز، لذا فإنّ هناك بعض الخطوات التي يجب اتباعها أو الاستعانة ببعضها للتمكّن من حلّ هذه المسائل بطريقة صحيحة، ومنها ما يأتي: فهم المسألة وتحليلها يُعدّ فهم السؤال نصف الإجابة، لذا يتطلّب حل المسائل الرياضية بدايةً قراءة السؤال بتمعّن وتفصيل لكلّ المعطيات فيه، وتجزئته حتى يسهل على المتعلّم تبسيط المسألة قدر الإمكان، بالإضافة إلى قراءة المسألة إلى نهايتها وتلخيصها. بالإضافة

كيفية حل النزاعات بين الطلاب تحدث النزاعات كجزء أساسي من الطبيعة البشرية، لترى الجيران والأطفال وأفراد العائلة الواحدة يتنازعون، وبالتأكيد ترى الطلاب في غرفة الصف الواحدة يتنازعون، فهم يتواجهون يوميًا ولساعات طويلة، وبالتالي تحدث النزاعات، وتاليًا الحلول التي عليك التوجه لها كي تُخفف من حدة هذه الصراعات بين الطلبة: هدّئ الأوضاع: دع طلابك يأخذون نفسًا عميقًا خاصّة أولئك الصّغار في السّن، فقد يحتاج طلابك إلى وقت للهدوء بعد النزاع. شارك واستمع وتحقّق: يحتاج طلابك إلى الاستماع لبعضهم البعض كي

كيفية حل المعادلات الرياضية بالتعويض تُستخدم طريقة التعويض لحل المعادلات الخطيّة جبريًّا بطريقة سهلة وبسيطة لإيجاد المتغيرات مجهولة القيم في المعادلة، وذلك باتّباع الخطوات الآتية: بسّط المعادلتين الخطيتين المعطاة في السؤال لأبسط صورة ممكنة. حل أيّ من المعادلتين لإيجاد قيمة المتغير الأول بدلالة المتغير الآخر، على سبيل المثال: إيجاد قيمة المتغير (س) بدلالة المتغير (ص)، ويُفضّل حل المعادلة الأبسط بين المعادلتين لسهولة الحساب والحصول على متغير بدلالة الآخر بصورة مبسطة. عوّض قيمة المتغير (س) التي

التركيز على الحل وليس المشكلة أثبت علماء الأعصاب أن العقل لا يمكنه أن يجد الحلول إذا كان التركيز على المشكلة، لأنه عند التركيز على المشكلة فإنّ التفكير السلبي يزيد والذي بدوره ينشط المشاعر السلبية في الدماغ، وهذه المشاعر تحجب الحلول المحتملة، لذلك يجب الحفاظ على الهدوء، فهو يساعد على التعرف على المشكلة أولاً، ثم الانتقال إلى التركيز حول الحل. تبسيط الأمور معظم الأشخاص لديهم ميول نحو جعل الأمور أكثر تعقيداً مما هي عليه، لذا لا بد من محاولة تبسيط المشكلة عن طريق تعميمها، من خلال إزالة جميع

حساب نصف قطر الدائرة من القوس يُعد طول القوس (بالإنجليزية: Arc Length) جزءًا من محيط الدائرة وهو المسافة التي تمر عبر الخط المنحني لجزء من محيط الدائرة، ويُسمى الخط المستقيم الواصل بين طرفي قوس الدائرة بالوتر، ويُمكن إيجاد نصف قطر الدائرة من القوس بطريقتين وهما كما يأتي: حساب نصف قطر الدائرة بمعلومية ارتفاع القوس وطول الوتر يُمكن حساب نصف قطر الدائرة بمعلومية ارتفاع القوس وطول الوتر من خلال المعادلة الآتية: نصف القطر= (ارتفاع القوس/2) (الوتر² / 8× ارتفاع القوس) وبالرموز: نق= (ل/2) (و² / 8 ل)

حساب مساحة قطعة أرض منتظمة بالمتر المربع يتساءل العديد حول كيفية إيجاد مساحة أرض منتظمة الشكل بالمتر المربع، وهنا، لا بد من تحديد الشكل أولًا، ومن ثم قياس المسافات والأبعاد اللازمة لحساب المساحة بوحدة المتر الطولي، ووفق المعادلات المرتبطة بكل شكل منتظم؛ علمًا بأنه يُمكن قياس المسافات والأبعاد بأي وحدة طولية معتمدة شريطة الانتباه إلى آلية التحويل بين وحدات الطول نفسها، وعدم الخلط بين أكثر من وحدة طول واحدة في أثناء العمليات الحسابية، إذ يجب أن يتم توحيد وِحَد الطول أولًا، والانتباه إلى أنّ

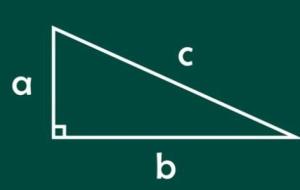
حساب محيط المثلث القائم وفيما يأتي كيفية حساب محيط المثلث قائم الزاوية (بالإنجليزية: Right Triangle): باستخدام القانون العام يمكن حساب محيط المثلث الذي أطوال أضلاعه أ، وب، وجـ من خلال حساب مجموع هذه الأطوال، وذلك كما يلي: محيط المثلث = أ ب جـ، حيث: أ، ب: هما طول ضلعي القائمة. جـ: هو طول الوتر في المثلث القائم. بالاستعانة بنظرية فيتاغورس ويمكن التعبير عن هذا القانون بطريقة أخرى، وذلك كما يلي: تنص نظرية فيثاغورس على أن مجموع مربعي طولي ضلعي الزاوية القائمة مساوٍ لمربع طول الوتر، أي أن: جـ²= أ²

كيفية حساب كفاءة استخدام الماء لفظًا تُعرّف كفاءة استخدام الماء (بالإنجليزيّة: (WUE) Water use efficiency) على أنّها كمية الكربون التي يتم استيعابها ككتلة حيويّة، أو حبوب منتجة لكلّ وحدة مياه يستخدمها المحصول،وعادةً ما يتم تحديد الكتلة الحيويّة على أنها وزن جاف وليس وزنًا جديدًا. يُوضح مفهوم كفاءة استخدام الماء العلاقة بين إنتاجيّة النبات واستخدام المياه، حيثُ يعتبر موضوع كفاءة استخدام المياه موضوعاً مهمّاً في الزراعة في المناطق شبه القاحلة، وذلك بسبب تزايد المساحات المرويّة وارتفاع الاحتياجات

طريقة حساب كثافة الجسم لحساب كثافة جسم ما لا بد من اتباع مجموعة من الإجراءات والخطوات، وفي ما يأتي توضيح لهذه الخطوات: حساب كتلة الجسم تُعرف الكتلة على أنها مقدار المادة المكوّنة للجسم (مقدار ما يحتويه الجسم من مادة)، وتُحسب الكتلة عن طريق وزن الجسم بالميزان الزنبركي أو العادي. وفي حال كان الجسم المراد حساب كتلته عبارةً عن سائل أو مسحوق ما، فلا بد من استخدام الوعاء المدرّج، وتحسب كتلته عن طريق وزن الوعاء وهو فارغ قبل وضع الجسم فيه ومن ثم يُطرح من الكتلة الكليّة للوعاء عند وضع الجسم فيه. حساب

كيفية حساب طاقة الفوتون يُمكن حساب طاقة الفوتون من خلال معادلة بلانك الآتية : طاقة الفوتون= ثابت بلانك × تردد الفوتون وبالرموز؛ ط الفوتون= ث × ت؛ حيث أن: ط: طاقة الفوتون، بوحدة الجول. ث: ثابت بلانك، وتبلغ قيمته 6.626 × 10 جول في الثانية. ت: تردد الفوتون، بوحدة الهيرتز. وبالرموز الإنجليزية؛ E = hν، حيث أن: E: إجمالي طاقة فوتون واحد. h: ثابت بلانك ν: تردد الفوتون. ومن هذه العلاقة يتضح أنّ تردد الفوتون يتناسب طردياً مع طاقته، أيّ أنّه كلّما تضاعف التردد تضاعفت طاقة الفوتون. ويجدر بالذكر أنّ جميع

طريقة حساب صافي الربح لمعرفة كيفية حساب الربح، فإنه يجب التطرق إلى المفاهيم الآتية أولًا: تكلفة الشراء: (بالإنجليزية: Cost Price) هي تكلفة شراء سلعة ما. تكلفة البيع: (بالإنجليزية: Selling Price) هي تكلفة بيع السلعة . يتحقق الربح إذا كانت تكلفة البيع أكبر من تكلفة الشراء، وعليه: الربح بشكل عام = تكلفة البيع - تكلفة الشراء، مع الإشارة إلى أن الخسارة تحدث إذا كانت تكلفة الشراء أكبر من تكلفة البيع. صافي الربح: يمكن إيجاد صافي الربح بالاستعانة بالقانون الآتي: صافي الربح = الربح الإجمالي - مجموع

كيفية حساب زاوية الانحراف تُعرّف زاوية الانحراف بأنّها الزاوية الناتجة عن الفرق بين زاويتيّ سقوط الشعاع الضوئي والانكسار داخل الوسط، بحيث تحدث زاوية الانكسار نتيجة انتقال الشعاع الضوئي من وسط له معامل انكسار يختلف عن معامل انكسار الوسط الذي انتقل إليه، وبالتالي فإنّ الفرق بين زاوية الانكسار الناتجة وبين زاوية السقوط يُمثل زاوية الانحراف ويُمكن تمثيله بالعلاقة الآتية: زاوية الانحراف = زاوية سقوط الشعاع - زاوية انكسار الشعاع وبالرموز: 𝜃ح = 𝜃س - 𝜃ن حيث إنّ: 𝜃ح: زاوية انحراف الشعاع الضوئي. 𝜃س:

كيفية حساب حجم الهرم الرباعي الناقص يُعرّف الهرم الرباعي (Square Pyramid) بأنّه شكل هندسي ثلاثي الأبعاد ، يتكون من أربعة جوانب مثلثية وقاعدة مربعة ورأس تلتقي عنده نهاية الجوانب المثلثية الأربعة، ويُسمى قمة الهرم، ويُطلق على الهرم الرباعي اسم الهرم خماسي الوجوه لامتلاكه أربعة جوانب وقاعدة، ويُمكن حساب حجمه من خلال الصيغة الرياضية الآتية: حجم الهرم الرباعي = ⅓ × مساحة قاعدة الهرم × ارتفاع الهرم وبما أنّ قاعدة الهرم الرباعي مربعة الشكل، فإنّ مساحة القاعدة المربعة = الطول × العرض، وأطوال أضلاع

كيفية حساب حجم الهرم الرباعيّ القائم يُعرّف الهرم الرباعيّ (Square Pyramid) بأنّه شكل هندسيّ ثلاثيّ الأبعاد يتكون من خمسة وجوه لذلك يُطلق عليه اسم الهرم خماسيّ الوجوه أيضًا، حيثُ يتكون من قاعدة مربعة، وأربعة أوجه جانبيّة مثلثة الشكل تلتقي جميعها عند نقطة في قمة الهرم تُسمى رأس الهرم. وإذا كانت جميع أطوال أضلاع الأوجه الجانبيّة للهرم الرباعيّ متساوية في الطول وارتفاع الهرم عاموديًا على منتصف القاعدة يُسمى الهرم الرباعيّ بالهرم الرباعيّ القائم، حيثُ تكون الأوجه الجانبيّة فيه عبارة عن مثلثات

كيفية حساب حجم الهرم الخماسي يُعرّف الهرم الخماسي (Pentagonal Pyramid) بأنّه شكل هندسي ثلاثي الأبعاد يتكون من قاعدة خماسية وخمسة أضلاع جانبية تلتقي جميعها عند نقطة قمة الهرم وتُسمى هذه النقطة برأس الهرم، ويُمكن حساب حجم الهرم الخماسي باستخدام الصيغة الرياضية الآتية: حجم الهرم الخماسي = ⅓ × مساحة قاعدة الهرم الخماسية × ارتفاع الهرم العمودي وبالرموز: ح = ⅓ × م × ع وبالإنجليزية: V = ⅓ × A × H حيث أنّ: ح (V): حجم الهرم الخماسي، ويُقاس بوحدة م³. م (A): مساحة قاعدة الهرم الخماسي، وتُقاس بوحدة م². ع