عبارات جميلة في الصباح للحبيب يأتي الصباح حاملًا معه نورًا يبعث الحياة، وشمس تشرق بالتفاؤل، وبداية يوم يمحو ما خلفه من آلام وأحزان، يُشعرك برغبة بالمضيّ والتقدّم، وأنّ الماضي ذهب ولن يعود، فترسم طريقًا جديدًا ببداية جديدة وأمل كبير، وتشارك عبارات جميلة فيه لحبيبك على النحو الآتي: أهديكم صباحًا جميلًا باسمًا عطره، ومقلة لا ترى في غيركم بدلًا، صباحكم فلّ إن شاء الله. أجمل الوجوه في الصباح ليست أحلاها خِلقة، وإنما أكثرها ابتسامة صباحكم مبتسمًا. لا شيء أجمل من لحظات النقاء والهدوء ، صوت العصافير
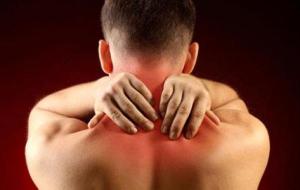
تشنج العضلات تشنج العضلات هو تقلصات أو تشنجات لا إرادية تحدث بشكلٍ مفاجئ في عضلة واحدة أو أكثر، وعادةً ما يحدث بعد التمرين، أو خلال الليل، ويستمر بضع ثوانٍ إلى عدة دقائق، فعندما يتم استخدام العضلات الإرادية، مثل: الأطراف، فإنها تنقبض وتنبسط أو تسترخي بشكلٍ متناوب خلال تحريك الأطراف ذهاباً وإياباً، أما العضلة التي تنقبض بشكل غير إرادي، ولا تنبسط أو تسترخي تسبب التشنج، وقد يشمل التشنج جزء من العضلة، أو العضلة بأكملها، أو عدة عضلات تعمل معاً. أسباب التشنج العضلي يوجد العديد من الأمور التي تتسبب
الإبداع الإبداع هو الإتيان بكل جديد، أو إعادة تقديم الأمور القديمة بشكل جديد وغريب، والتعامل مع الأشياء المألوفة بطريقة غير مألوفة، إضافة إلى دمج الآراء بصورة جديدة، وللإبداع أربعة مكوّنات، وهي=== العمل الإبداعي، والعملية الإبداعية، والشخص المبدع، والموقف الإبداعي، كما أنّ هناك مراحل يمر بها الإبداع، وسنتناول في مقالنا هنا هذه المراحل بالتفصيل. مراحل عملية الإبداع مرحلة الإعداد أو التحضير ينغمس الفرد المبدع أو الفريق المبدع في هذه المرحلة في المشكلة، فهي مرحلة جمع للمعلومات، أما في عمل الفريق
أدعية فجر الجمعة لم يثبت لدعاء فجر يوم الجمعة فضيلة خاصة، ولكنّ وقت السحر وهو الوقت الذي يسبق الفجر من أوقات الإجابة، وفيما يأتي بعض الأدعية المأثورة وغير المأثورة التي يمكن الدعاء بها فجر الجمعة: (اللَّهُمَّ أَصْلِحْ لي دِينِي الذي هو عِصْمَةُ أَمْرِي، وَأَصْلِحْ لي دُنْيَايَ الَّتي فِيهَا معاشِي، وَأَصْلِحْ لي آخِرَتي الَّتي فِيهَا معادِي، وَاجْعَلِ الحَيَاةَ زِيَادَةً لي في كُلِّ خَيْرٍ، وَاجْعَلِ المَوْتَ رَاحَةً لي مِن كُلِّ شَرٍّ). (اللَّهُمَّ إنِّي أَعُوذُ بكَ مِنَ العَجْزِ،
الروزماري وزيت الزيتون يدخل الروزماري وزيت الزيتون في العديد من العلاجات العشبية والمنزليّة لعلاج الشعر التالف، حيث يحفّز الرزماري نمو الشعر، ويحميه من الضرر، ويعدّ زيت الزيتون من المواد المغذية للشعر، ولتطبيق خلطة الروزماري مع زيت الزيتون يتمّ تسخين ربع كوب من زيت الزيتون في مقلاة، حتى يصبح دافئاً، ثمّ إضافة خمس قطرات من زيت الروزماري، ثمّ تطبيق الخليط الناتج على الشعر، وتغطية الشعر بغطاء بلاستيكيّ، وتركه لمدّة عشرين دقيقة على الأقل، ثمّ غسله بالشامبو، ومن الممكن حفظ الزائد من الخليط في
وحدات الإدخال وحدات الإدخال (Input Devices) هي الوحدات التي تُستخدم في جهاز الحاسوب من أجل إدخال البيانات والمعلومات إلى الجهاز، وفي ما يأتي عدد من هذه الوحدات ووظيفة كل منها في جهاز الحاسوب: لوحة المفاتيح: (Keyboard)؛ وتُعد المكوّن الأكثر شهرةً في إدخال البيانات للحاسوب من أحرف وأرقام وغيرها، وتُشبه في تصميمها الآلة الكاتبة مع وجود بعض الأزرار الإضافية. الفأرة: (Mouse)؛ ويتحكم هذا المكوّن في حركة المُؤشّر، ويضم الماوس زر أيمن، وزر أيسر، وعجلة صغيرة تقع بين الأزرار. الماسح الضوئي: (Scanner)؛
الشركة الشركة (بالإنجليزيّة: Company) هي رابطة تمّ تشكيلها وتنظيمها من أجل القيام بأعمال تجاريّة، وتُقسم الشركة إلى مجموعة من الأنواع، من أهمّها شركات الملكيّة الفرديّة، والمسؤوليّة المحدودة، والعامة المحدودة، وشركات الشراكة وغيرها، وتُعرَّف الشركة بأنّها تشكيل شخص أو مجموعة أشخاص لأعمال تجاريّة، مثل شركات الشحن. من التعريفات الأخرى للشركة أنّها تجمع أفراد من أجل تنفيذ عمل مُشترك بينهم، سواءً لأغراض اجتماعيّة أو تجاريّة. كيفيّة تأسيس شركة يسعى الكثير من الأفراد إلى تأسيس شركات لتطبيق أعمال في
من هي عبلة كامل؟ عبلة كامل هي ممثلة مصرية، وفيما يأتي أبرز المعلومات عنها: الاسم الحقيقي: عبلة كامل محمد عفيفي. الاسم الفني: عبلة كامل. المهنة: ممثلة مصرية. تاريخ الولادة: 18 يوليو 1957. مكان الولادة: القاهرة/ جمهورية مصر العربية. الجنسية: مصرية. مكان الإقامة: مصر. كيف نشأت عبلة كامل؟ ولدت عبلة كامل في 18 يوليو عام 1957 في إيتاي البارود التي تقع في محافظة البحيرة في جمهورية مصر العربية، وعاشت طفولتها فيها، ثم التحقت بكلية الآداب بقسم المكتبات في جامعة القاهرة وتخرجت منه في عام 1984، وبعد