كيفية حساب محيط المثلث القائم

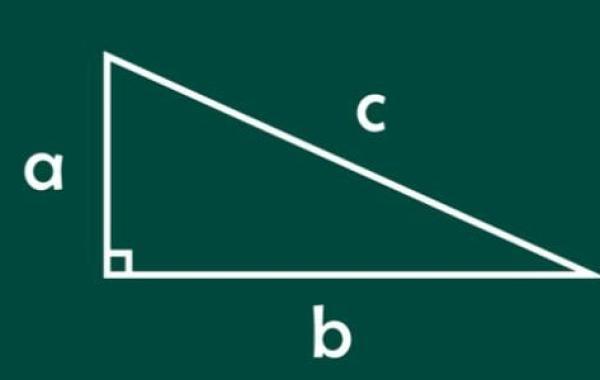
حساب محيط المثلث القائم

وفيما يأتي كيفية حساب محيط المثلث قائم الزاوية (بالإنجليزية: Right Triangle):

باستخدام القانون العام

يمكن حساب محيط المثلث الذي أطوال أضلاعه أ، وب، وجـ من خلال حساب مجموع هذه الأطوال، وذلك كما يلي:

• محيط المثلث = أ ب جـ، حيث:
  • أ، ب: هما طول ضلعي القائمة.
  • جـ: هو طول الوتر في المثلث القائم.

بالاستعانة بنظرية فيتاغورس

ويمكن التعبير عن هذا القانون بطريقة أخرى، وذلك كما يلي:

• تنص نظرية فيثاغورس على أن مجموع مربعي طولي ضلعي الزاوية القائمة مساوٍ لمربع طول الوتر، أي أن: جـ²= أ² ب²، وبالتالي فإن جـ = (أ² ب²)√.
• بتعويض قيمة الوتر في قانون المحيط: محيط المثلث القائم = أ ب جـ فإن محيط المثلث هو:
  • محيط المثلث القائم = أ ب (أ² ب²)√، وذلك لحساب محيط المثلث دون معرفة الوتر؛ حيث إن:
    • أ، ب: طول ضلعي القائمة.

أمثلة على حساب محيط المثلث قائم الزاوية

وفيما يأتي أمثلة متنوعة على حساب محيط المثلث قائم الزاوية:

• المثال الأول: مثلث قائم الزاوية أضلاعه هي: 3، 4، 5سم، جد محيطه.

الحل:

• بتطبيق القانون: محيط المثلث = مجموع أطوال أضلاعه= أ ب جـ = 3 4 5 = 12سم.

• المثال الثاني: مثلث قائم الزاوية أضلاعه هي: 6، 8، 10م، جد محيطه.

الحل:

• بتطبيق القانون: محيط المثلث = مجموع أطوال أضلاعه= أ ب جـ = 6 8 10 = 24م.

• المثال الثالث: مثلث قائم الزاوية طول أحد ضلعيه (ب) يساوي 4/3 من طول الضلع الآخر (أ)، وطول الوتر(جـ) يساوي 30 م، فما هو طول ضلعي القائمة، وما محيط المثلث القائم؟

الحل:

• نفرض أن طول الضلع (أ) = س، وبالتالي فإن طول الضلع ب = 4/3×س.
• تطبيق نظرية فيثاغورس لإيجاد طول ضلعي القائمة كما يلي:
  • جـ² = أ² ب²، 30² =س² (4/3×س)²، س² (16/9)س²=900، 25/9 س²=900، وبحل المعادلة ينتج أن: س= 18م، وبالتالي فإن طول الضلع (أ) = 18م.
• طول الضلع (ب) = 4/3×س = 4/3×18= 24م.
• محيط المثلث = مجموع أطوال أضلاعه، ويمكن إيجاد المحيط كما يلي:
  • محيط المثلث = أ ب جـ = 18 24 30 = 72 م.

• المثال الرابع: ما هو محيط المثلث القائم الذي طول الوتر فيه (جـ) يساوي 8سم، وطول أحد ضلعيه (أ) يساوي 5سم؟

الحل: محيط المثلث القائم = مجموع أطوال أضلاعه.

• لحساب المحيط فإنه يجب إيجاد طول الضلع الثالث (ب) للمثلث، وذلك باستخدام نظرية فيثاغورس كما يلي:
  • جـ² = أ² ب²، 8² = 5² ب²، 64 = 25 ب²، ومنه: ب= 39√= 6.24 سم.
• بعد إيجاد طول الضلع الثالث يمكن حساب محيط المثلث القائم كما يلي:
  • محيط المثلث = أ ب جـ = 5 6.24 8= 19.24سم.

• المثال الخامس: إذا كان طول أحد ضلعي المثلث القائم يزيد عن طول الضلع الآخر بمقدار 200سم، وطول الوتر (جـ) فيه يساوي 1000سم، فما هو طول ضلعي القائمة، وما هو محيط المثلث القائم؟

الحل:

• لنفرض أن طول الضلع الأول (أ)= س، وبما أن طول الضلع الثاني (ب) يزيد عن طول الضلع الأول بمقدار 200، فإن ب= 200 س.
• يمكن تطبيق نظرية فيثاغورس لإيجاد طول ضلعي القائمة كما يلي:
  • جـ² = أ² ب²، (1000)² = س² (س 200)²، وبفك الأقواس وترتيب المعادلة ينتج أن: 2س² 400س- 960,000=0، وبحل هذه المعادلة التربيعية ينتج أن: س= 600، وس= -800، وبما أن س تمثل طول الضلع أ، ولا يمكن للطول أن يكون سالباً، فإنه يجب إهمال قيمة س= -800.
• طول الضلع أ يساوي 600سم، وطول الضلع ب= س 200= 200 600 = 800 سم.
• محيط المثلث القائم يساوي مجموع أطوال أضلاعه، ويمكن إيجاده كما يلي:
  • محيط المثلث = أ ب جـ = 600 800 1000= 2,400 سم.

• المثال السادس: ما هو محيط المثلث قائم الزاوية الذي طول الوتر فيه 50سم، علماً أن المثلث متساوي الساقين؟

الحل: محيط المثلث يساوي مجموع أطوال أضلاعه، ولحساب طول هذه الأضلاع يجب اتباع ما يلي:

• يمكن إيجاد طول الضلعين المتساويين اللذين يمثلان ضلعي القائمة باستخدام نظرية فيثاغورس، وذلك كما يلي:
  • الوتر²= (الضلع الأول)² (الضلع الثاني)²، ومنه: 50² = 2×(طول أحد الضلعين)²، وذلك لأن الضلعين متساويان في الطول، ومنه: 2500 = 2×طول أحد الضلعين²، وبالقسمة على (2)، وأخذ الجذر التربيعي للطرفين ينتج أن طول الضلعين المتساويين= 1250√ سم.
• أصبحت جميع أطوال أضلاع المثلث القائم معروفة، وبالتالي يمكن إيجاد المحيط كما يلي:
  • محيط المثلث = الوتر طول ضلعي القائمة = 50 (2×1250√)= 120.7سم تقريباً.

• المثال السابع: مثلث قائم أ ب جـ فيه طول الوتر أج = 6سم، وطول الضلع أب= (5س)√، وطول الضلع ب جـ= س، فما هو محيطه؟

الحل:

• يمكن استخدام نظرية فيثاغورس لإيجاد قيمة س، وذلك كما يلي:
  • أج² = ب جـ² أ ب²، 6² = (5س√)² س²، 36 = 5س س²، س² 5س-36=0، وبتحليل المعادلة التربيعية إلى عواملها فإن: (س 9)(س-4)=0، وبالتالي فإن س لها قيمتان، وهما: س= -9، وس= 4، والقيمة الأولى تُهمل، وذلك لأن الطول لا يمكن أن يكون سالباً.
• طول الضلع ب جـ =4سم، أب= (5س)√ = (5×4)√ = (5)√2 سم.
• محيط المثلث القائم يساوي مجموع أطوال أضلاعه، ويمكن إيجاده كما يلي:
  • محيط المثلث = أب ب جـ أ جـ = (5)√2 4 6= 10 5√2 سم.

• المثال الثامن: مثلث متساوي الساقين وقائم الزاوية فيه طول الوتر 2√8 سم، ما هو محيطه؟

الحل: بما أن المثلث متساوي الساقين، وقائم الزاوية، فإنه يمكن إيجاد طول الضلعين المتساويين اللذين يمثلان ضلعي القائمة كما يلي:

• الوتر²= (الضلع الأول)² (الضلع الثاني)²، ومنه: (2√8)²= 2×(طول أحد الضلعين)²، وذلك لأن الضلعين متساويان في الطول، ومنه: 192= 2×طول أحد الضلعين²، وبقسمة الطرفين على (2)، وأخذ الجذر التربيعي للطرفين ينتج أن: طول الضلعين المتساويين= 8 سم.
• محيط المثلث القائم = 2×طول أحد ضلعي القائمة طول الوتر = 2×8 2√8= 16 2√8 سم.