تعليم

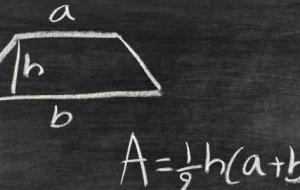
مساحة شبه المنحرف غير المنتظم يُعرّف شبه المنحرف غير المنتظم (بالإنجليزية: irregular trapezoid) بأنّه شبه منحرف أضلاعه الجانبية غير متوازية وغير متساوية في الطول، ويُمكن حساب مساحته بعدة طرق على النحو الآتي: حساب مساحة شبه المنحرف غير المنتظم معلوم الأبعاد يُمكن حساب مساحة شبه المنحرف غير المنتظم معلوم الأبعاد من خلال استخدام المعادلة الرياضية الآتية: مساحة شبه المنحرف غير المنتظم = ½ × مجموع القاعدتين × الارتفاع وبالرموز: م = ½ × (ق1 ق2) × ع حيث إنّ: م: مساحة شبه المنحرف غير المنتظم، ويُقاس

حساب مساحة شبه المنحرف القائم يمثّل شبه المنحرف القائم (بالإنجليزية: Right Trapezoid) حالة خاصة أو نوعاً من أنواع شبه المنحرف ، وهو يتميز بامتلاكه لزاويتين قائمتين متجاورتين، ويمكن حساب مساحته باستخدام القانون العام لحساب مساحة شبه المنحرف، وهو: مساحة شبه المنحرف= ½×(مجموع القاعدتين)×الارتفاع وبالرموز: م= ½×(ق 1 ق 2 )×ع حيث أن: م: مساحة شبه المنحرف. ق 1 ، ق 2 : طول قاعدتي شبه المنحرف. ع: ارتفاع شبه المنحرف. أمثلة متنوعة على حساب مساحة شبه المنحرف القائم وفيما يأتي أمثلة متنوعة على حساب مساحة

قانون مساحة الهرم يمكن تعريف المساحة الجانبية للهرم (بالإنجليزية: Lateral Surface Area) بأنها مجموع المساحات للأوجه المثلثة الجانبية، أو كامل الأوجه باستثناء مساحة القاعدة، أما المساحة الكلية (بالإنجليزية: Total Surface Area) فتتمثّل بمجموع المساحة الجانبية، ومساحة القاعدة، ويمكن إيجاد المساحة الجانبية، والكلية باستخدام الصيغ الآتية: المساحة الجانبية = 1/2 × محيط القاعدة × الارتفاع الجانبي. المساحة الكلية = المساحة الجانبية مساحة القاعدة. يمكن حساب مساحة الهرم الكلية حسب شكل قاعدته وفق

مساحة سطح منشور رباعي ذو قاعدة مستطيلة يعد المنشور من المجسمات الهندسية ثلاثية الأبعاد التي يندرج تحتها العديد من الأنواع، إحداها هو المنشور الرباعي ذو القاعدة المستطيلة (بالإنجليزية: Rectangular Prisim)، ويمتاز هذا النوع بأن له 6 أوجه جميعها مستطيلة الشكل، بينما كل وجهين متقابلين فيه يتطابقان تمامًا في أبعادهما، فإنّ شكل مقطعه العرضي على طول محوره مستطيل أيضًا، وبالإضافة إلى ما سبق، فإنّ له 8 رؤوس، و12 حرفًا، وقد يكون إما قائمًا أو مائلًا، و يُطلق عليه في العموم اسم متوازي المستطيلات

طرق حساب مساحة شبه المنحرف يمكن حساب مساحة شبه المنحرف باستخدام أحد القوانين أو الطرق الآتية: عند معرفة طول القاعدتين والارتفاع وذلك بتطبيق القانون: مساحة شبه المنحرف = ½ × (طول القاعدة الأولى طول القاعدة الثانية) ×الارتفاع وبالرموز: م= ½× (أ ب)×ع حيث إنّ: م: مساحة شبه المنحرف. أ: طول القاعدة السفلية. ب: طول القاعدة العلوية. ع: الارتفاع. باستخدام صيغة هيرون وذلك عند معرفة أطوال جميع الأضلاع دون معرفة الارتفاع، والتي تنص على أنّ: م=((و-أ)(و-ب)(و-أ-ج)(و-أ-د))√×(أ ب)/(|أ-ب|) حيث إنّ: م: مساحة شبه

مسائل محلولة على الأرقام المعنوية تعرف الأرقام المعنوية بأنها عدد الأرقام الموجودة في المنازل حيث تشمل هذه الأرقام الأعداد من 0 إلى 9 وتتصف بقدرتها على إعطاء نتيجة دقيقة، يتم استخدامها من قبل العلماء والمهندسين لإعطاء قياسات دقيقة عند الاستخدام؛ فمثلاً: عند قياس الوزن أو الطول أو الحجم وغيرها من القياسات، وهذه بعض المسائل المحلولة على الأرقام المعنوية: إيجاد عدد الأرقام المعنوية مثال: جد عدد الأرقام المعنوية في الأسئلة التالية:الحل: الأسئلة عدد الأرقام المعنوية التفسير 3.205 4 أي عدد غير صفري

تمارين على حساب المساحة الكلية للأسطوانة يُمكن حساب المساحة الكليّة لسطح الأسطوانة من خلال جمع المساحة الجانبية للأسطوانة، مع ضعفي مساحة القاعدة، كما في القانون الآتي: المساحة الكلية للأسطوانة= المساحة الجانبية 2 × مساحة القاعدة ومنه؛ المساحة الكلية للأسطوانة = (2 × π × نق) × ع 2 × (π× نق²) المساحة الكلية للأسطوانة = (2 × π × نق) × (نق ع) إذ إن: نق: نصف قطر الأسطوانة. ع: ارتفاع الأسطوانة. مثال (1): احسب المساحة الكلية للأسطوانة إذا علمت أن المساحة الجانبية لها= 300 سم²، وأن مساحة القاعدة= 200

أمثلة على حساب القوة الكهربائية وفيما يأتي بعض الأمثلة على حساب القوة الكهربائية: مثال 1: شحنتان تحمل الأولى منهم شحنة مقدارها 4×10 كولوم، والثانية 6×10كولوم، وتفصل بينهما مسافة 3×10م في الفراغ، باعتبار ك=9*10، فما مقدار القوة المتبادلة بينهما؟ الحل: باستخدام قانون كولوم: ق= ك×(ش 1 ×ش 2 )/ف ق= 9×10×4×10×6×10/(3×10) ق= 24× 10 نيوتن. مثال 2: ثلاث شحنات نقطية تقع على خط مستقيم، تبلغ شحنة الأولى ش1= 2×10 كولوم، والثانية ش2= 1×10، والثالثة ش3=-3×10، وتبلغ المسافة بين الشحنة الأولى والشحنة الثانية

مسائل على محيط المستطيل يُمكن حساب مُحيط المستطيل باتّباع الأمثلة الآتية: محيط مستطيل معلوم الأبعاد المثال الأول: احسب محيط المستطيل الذي عرضه 6.21 سم وطوله 8.7 سم. الحل: عوّض في قانون محيط المستطيل لإيجاد المحيط على النحو الآتي: محيط المستطيل = 2 × (الطول العرض) محيط المستطيل = 2 × (8.7 6.21) محيط المستطيل = 2 × 14.91 محيط المستطيل = 29.82 سم. المثال الثاني: احسب محيط المستطيل، إذ علمتَ أنّ عرضه 11.5 سم وطوله يساوي ضعف عرضه. الحل: جد طول المستطيل = 2 × العرض = 2 × 11.5 = 23 سم عوّض في قانون

مسائل على قانون مساحة شبه المنحرف ندرج فيما يأتي أمثلة متنوعة على حساب مساحة شبه المنحرف : إيجاد مساحة شبه المنحرف بمعلومية أبعاده المثال (1): احسب مساحة شبه المنحرف الذي طول قاعدته السفلية 14 سم، وطول قاعدته العلوية 5 سم، وارتفاعه 10 سم. الحل: تُكتب المعطيات: طول القاعدة العلوية = 5 سم طول القاعدة السفلية = 14 سم الارتفاع = 10 سم تُعوض المعطيات في قانون مساحة شبه المنحرف على النحو الآتي: مساحة شبه المنحرف = ½ × (طول القاعدة السفلية طول القاعدة العلوية) × الارتفاع مساحة شبه المنحرف = ½ × (14

مسائل على طاقة وضع الجاذبية طاقة وضع الجاذبية (بالإنجليزية: Gravitational Potential Energy) [١] هي [٢] الطاقة التي يكتسبها الجسم نتيجة وجوده في موقع ما في حدود مجال الجاذبية ، والتي ترتبط بقوة الجاذبية ولأنّ القوة المطلوبة لرفع الجسم إلى الارتفاع (ع) تساوي وزنه، فإنّ طاقة وضع الجاذبية تساوي وزن الجسم مضروبة في الارتفاع، والوزن يساوي كتلة الجسم مضروب في تسارع الجاذبية الثابت ومقداره 9.8 م/ث²، ويُعبر عن طاقة وضع الجاذبية بالمعادلة التالية: طاقة وضع الجاذبية = كتلة الجسم × ثابت تسارع الجاذبية ×

مسائل على حساب الوسيط الحسابي قيمة الوسيط لمجموعة البيانات الفردية مثال 1: إيجاد قيمة الوسيط في مجموعة البيانات الآتية: 3, 7, 6, 9, 2, 1, 8 الحل: رتب الأعداد تصاعديًّا (1, 2, 3, 6, 7, 8, 9). عد مجموعة القيم وهي 7 أرقام إذن تعتبر أرقامًا فردية. حدد القيمة الوسطى، وهي التي تفصل بين 3 أرقام من يمينها ويسارها؛ فتكون القيمة الوسطى لمجموعة البيانات 1, 2, 3, 6, 7, 8, 9). الوسيط = 6. مثال 2: إيجاد قيمة الوسيط لمجموعة البيانات الآتية: 22, 43, 27, 14, 50 الحل: رتب الأعداد ترتيبًا تنازليًّا (50, 43, 27,

مسائل على حساب المنوال ندرج فيما يأتي أمثلة على حساب المنوال: المنوال عند وجود منوال واحد في مجموعة البيانات المثال (1): احسب المنوال لمجموعة الأرقام الآتية: 15، 5، 3، 17، 1، 9، 6، 5، 17، 11، 7، 5، 13. الحل: جد المنوال من خلال ترتيب الأرقام تصاعديًا أو تنازليًا ثم إيجاد الرقم الأكثر تكرار من بين المجموعة، وذلك على النحو الآتي: رتب الأرقام تصاعديًا: 1، 3، 5، 5، 5، 6، 7، 9، 11، 13، 15، 17، 17. لاحظ بأنّ العدد الأكثر تكرار في مجموعة الأرقام هو العدد 5 وقد تكرّر ثلاث مرات. وبالتالي فإنّ المنوال

حجم متوازي المستطيلات حجم متوازي المستطيلات هو قياس الفضاء الذي يشغل ما بداخل متوازي المستطيلات، وبما أن متوازي المستطيلات له ثلاثة أبعاد وهي الطول والعرض والارتفاع، فإن قياس حجم متوازي المستطيلات يكون ناتج ضرب الثلاثة أبعاد هذه، حيث إن ضرب كل من الطول بالعرض يعطينا قيمة مساحة قاعدة متوازي المستطيلات، بينما ضربها مع قيمة ارتفاع المتوازي المستطيلات يعطي نتيجة حجم هذا المتوازي المستطيلات، أما وحدة قياس الحجم هي متر مكعب (م3). الصيغة الرياضية لحجم متوازي المستطيلات : حجم متوازي المستطيلات= الطول

حجم المستطيل يتكون المستطيل من قاعدة ووجه علوي، ووجوه جانبية مستطيلة، ويُصنف المنشور المستطيل كشكل هندسي ثلاثي الأبعاد ، له ستة أوجه متكونة من مستطيلات، وعند حساب حجم المستطيل، يمكن أن نتخيله على شكل وعاء، ونريد ملؤه بالماء، فتكون كمية الماء التي ستملأ الوعاء هي الحجم ، أو بمعنى آخر هي المساحة الكلية بداخل المستطيل . يمكن التعبير عن الحجم بعدة وحدات، وتعتبر وحدة المتر مكعب (m³) هي الوحدة الأساسية، إلى جانب السانتيمتر مكعب (cm³)، ولتر (L)، والمليلتر (ml) . معادلة حجم المستطيل تُكتب معادلة حجم

كيفية حساب حجم المخروط يمكن حساب حجم المخروط اعتمادا على نوعه، وذلك كما يلي: قانون حجم المخروط القائم فيما يأتي قانون حساب حجم المخروط القائم بالكلمات والرموز: حجم المخروط= 1/ 3 × مساحة القاعدة الدائرة × الارتفاع. بالرموز: حجم المخروط = 1/ 3× π × نق²× ع. قانون حجم المخروط الناقص فيما يأتي قانون حساب حجم المخروط الناقص بالكلمات والرموز: حجم المخروط الناقص= 1 /3 × (مساحة القاعدة الأولى مساحة القاعدة الثانية الجذر التربيعي لناتج (مساحة القاعدة الأولى × مساحة القاعدة الثانية) × الارتفاع. وبالرموز:

مسائل حسابية على المنوال والوسيط والوسط الحسابي والمدى يُمكن دراسة الأمثلة الآتية في حساب المنوال والوسيط والوسط الحسابي والمدى: مثال (1): أوجد المنوال والمتوسط الحسابي والوسيط والمدى لمجموعة القيم (13، 18، 13، 14، 13، 16، 14، 21، 13). الحل: رتب الأعداد تصاعديًا: (13، 13،13،13، 14، 14، 16، 18، 21) المنوال : هو القيمة الأكثر تكرارًا وهي 13. الوسيط: هو القيمة الوسطى وهي 14. الوسط الحسابي: هو مجموع القيم مقسوما على عددها (13 13 13 13 14 14 16 18 21) /9) حيث أن الناتج هو 15. المدى: هو الفرق بين

مسائل رياضيات مع الحل عن الجمع والطرح يُعد الجمع والطرح إحدى العمليات الحسابية للتعامل مع الأرقام، كما أنّ الطرح عملية عكسية للجمع، وندرج فيما يأتي بعض المسائل الرياضية عن الجمع والطرح: المثال الأول: إذا علمتَ أنّ عدد طالبات الصف الرابع الابتدائي 15 طالبة، وعدد الطلاب 11 طالب، فما هو عدد طلاب الكلي للصف الرابع الابتدائي؟ الحل: نُلاحظ من المطلوب أنّ العملية الحسابية هي عملية جمع. تُرتب الأعداد عموديًا: 15 11 ـــــــ 26 إذًا في الصف الرابع 26 طالبًا. المثال الثاني: جد ناتج طرح المعادلة

مزايا الملاحظة في البحث العلمي من مزايا الملاحظة في البحث العلمي ما يأتي: المباشرة والبساطة الميزة الرئيسية للملاحظة هي مباشرتها، يمكننا جمع البيانات وقت حدوثها، فيمكن للباحث ببساطة أن يشاهد الأفراد يتصرفون ويتحدثون، في حين أن المشاركين في الاستطلاع قد يكون لديهم ذاكرة ضبابية أو متقطعة حول الأحداث التي حدثت في الماضي البعيد، لكن المراقب (المُلاحظ) يدرس الأحداث عند حدوثها. تأسيس الفرضيات الملاحظة هي أحد الأسس الرئيسية لصياغة الفرضية ، من خلال مراقبة الظاهرة بشكل مستمر، كل هذا يساعد الباحث في

مميزات المقابلة في البحث العلمي يوجد ‏للمقابلة مميزات كغيرها من أدوات البحث العلمي نذكرها، فيما يلي: ‏تساعد المقابلة الباحث على جمع المعلومات بدقة أكثر، في حال كان المبحوث لا يعرف الكتابة أو القراءة. ‏تساعد المقابلة الباحث على جمع المعلومات بشكل أسرع، قبل أن يتأثر المبحوث بالظروف الخارجية والآراء من حوله. ‏تساعد المقابلة الباحث ليس فقط على جمع المعلومات المكتوبة، بل أيضاً تساعد على الحصول على المعلومات الجسدية كطريقة تصرف البحوث وحركاته الجسدية عند سؤاله. ‏تساعد المقابلة الباحث على الانخراط في

مزايا المركزية الإدارية فيما يأتي توضيح لأهم مزايا تطبيق المركزية الإدارية: تتميز المركزية الإدارية بوضوح عملية صنع القرار . تعمل المركزية الإدارية على التنفيذ المبسط للسياسات والمبادرات. تسهم في السيطرة على الاتجاه الاستراتيجي. يسهم تطبيق المركزية الإدارية كأسلوبٍ إداري في تقليل النفقات المصروفة. تضمن توزيع العمل بشكل عادل وبدون تحيز. تعزز المرونة أثناء حالات الطوارئ أو الأزمات. تقلل من فرصة تكرار العمل نفسه من قبل أشخاص مختلفة. تسهيل عملية توزيع المهام. عيوب المركزية الإدارية فيما يأتي توضيح

يُعرف المجهر الإلكتروني بالمجهر الذي يستخدم حزم من الإلكترونات لتكبير الأشياء، وعرضها على شاشة رقمية، وأجهزة كمبيوتر التي تستخدم لتحليل الصور، كما يختلف عن المجهر الضوئي الذي يستخ دم جزيئات الضوء أو الفوتونات لتكبير الأشياء، ويتميز المجهر الإلكتروني بعدة ميزات، إلا أن له بعض العيوب أيضاً. مزايا المجهر الإلكتروني تشمل مزايا المجهر الإلكتروني ما يلي: قدرة عالية على تكبير الأشياء يستطيع المجهر الإلكتروني تكبير الأشياء بدقة عالية، ويعود السبب إلى استخدامه لحزم الإلكترونات، لذلك فهو يستطيع تحليل

الخشب البلاستيكي WPC تصنع ألواح الخشب البلاستيكي بتقنية تعتمد على خلطات خاصة لمواد مع ألياف طبيعية من الخشب والمنتجات الزراعية الثانوية لتخلط بمواد كيميائية حتى تتجانس مع البلاستيك للحصول على مزايا مزدوجة تجمع بين خواص البلاستيك والخشب، وهو مزيجٌ مبتكر حيث يقوم الخشب بحماية ألواح البلاستيك من الأشعة فوق البنفسجية بينما يقوم البلاستيك بحماية الخشب من الحشرات والماء ليتمتع المنتج بمتانة الخشب وصلابة ونسيج البلاستيك، ويتم صنعه من خلال مزج البوليمر البكر المقاوم للاحتراق مع مسحوق الخشب بمواد

مزايا الجبس بورد الجبس بورد أو ألواح الحبس (بالإنجليزية: Gypsum board) هي عبارة عن مواد البناء مكونة من الجبس وصفائح الورق، ولتصنيعه، يتم استخراج الجبس ثم طحنه إلى مسحوق وتسخينه حتى يخضع لعملية تسمى التكليس، والتي تحدث عندما يتم إخراج 75% من المياه المجمعة كيميائيًا، وبمجرد ضغطه وتغليفه بين واجهات الورق يصبح عبارة عن سطح جدار متين جاهزًا للطلاء، تم استخدام الجبس منذ العصور القديمة، لكن الجبس بورد جاء من لوح (Sackett) الذي تم اختراعه في أواخر القرن التاسع عشر، وعلى مدار العقدين التاليين، تم