تعليم

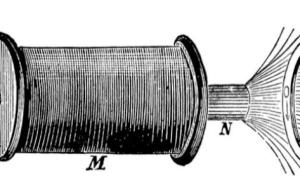
أهم تطبيقات قوانين نيوتن في حياتنا وضع العالم نيوتن القوانين الأساسية في الميكانيكا، والتي اشتهرت بقوانين نيوتن في الحركة، كما قدم العديد من الإنجازات التي أفادت البشرية، و تتعدد مجالات استخدامات قوانين نيوتن في مجالات الحياة اليومية ، ومن أهم هذه التطبيقات ما يأتي: الصاروخ يُعدّ مبدأ عمل الصاروخ أحد التطبيقات الشائعة لقانون نيوتن الثالث ، حيث ينطلق الصاروخ إلى أعلى بسرعة عالية كرد فعل للغازات المنبعثة من الأسفل نتيجة الاحتراق الذي يؤدي إلى ارتفاع درجات الحرارة التي تؤدي بدورها إلى تمدد

تطبيقات طبية تكمن فائدة البحث في قوانين الغازات ، في أن استخدامات قوانين الغاز متنوعة في العديد من المجالات منها المجال الطبي، ويختلف الاستخدام بحسب اختلاف قانون الغاز: قانون بويل؛ يُستفاد منه في الأماكن العميقة والتجاويف المغلقة في جسم الإنسان لمعرفة تأثير الغازات فيها وحساب التغير بالحجم على ارتفاعات مختلفة، وحساب حجم الغازات الكلي داخل الصدر، ويتضح مبدأ القانون في شرح حالة الغواص عند خروجه من أعماق البحر وعند حبسه لأنفاسه وكيف للغازات أن تتمدد في رئتيه وتسبب انتفاخها، كذلك أي شخص مصاب بما

تطبيقات عملية من حياتنا على المعادلات الخطية تستخدم المعادلات الخطية (بالإنجليزية: Linear equations) متغيراً واحداً أو أكثر من متغير، بحيث يعتمد أحد المتغيرات على الآخر، ويمكن تمثيل أي كمية غير معروفة القيمة بمعادلة خطية، وتكون الصيغة الرياضية القياسية للمعادلة الخطية ص = ( م × س ). يمكن استخدام المعادلات الخطية في التطبيقات الحياتية اليومية، مثل حساب معدل المسافات المقطوع للمركبات، أو حساب الميزانية، أو توقع أرباح مشروع تجاري معين، أو تقدير التكاليف، وفيما يلي بعض الأمثلة على هذه التطبيقات

أهم التطبيقات على قانون نيوتن الثاني لقد قام العالم إسحاق نيوتن بالتَّوسُع والتَّعمُق في الأعمال السابقة لاستاذ الفيزياء في جامعة أوريغون جاليليو غاليلي، حيث إن جاليليو غاليلي كان هو مَن قَام بتطوير أول القوانين الدقيقة للحركة، حيث أظهرت قوانينه وتجاربه أن جميع الأجسام تتسارع بنفس المُعدَّل بغض النظر عن حجم هذه الأجسام وكُتلتها، كذلك قام اسحاق نيوتن بالتَّوسُع والتَّعمُق في أعمال رينيه ديكارت والذي كان قد نشر مجموعة من قوانين الطبيعة في عام 1644م. يتم تطبيق قانون الثاني في الغالب من قبل

الميزان الحسّاس يعد الميزان الحسّاس من الأجهزة التي تستخدم كتطبيق عملي على قانون لينز خصوصًا في مختبرات الكيمياء، ويتمحور عمل هذا الميزان على إيقاف اهتزازه عند وضع جسم على كفته. ويحتوي هذا الميزان على قطعة معدنية موصولة بذراع التوازن وموضوعة بين قطبي مغناطيس من نوع حذوة الحصان، وتتحرك القطعة المعدنية داخل المجال المغناطيسي نتيجة لتأرجح ذراع الميزان، لينشأ عندها تيارات تولد مجالًا مغناطيسيًا في اتجاه معاكس لاتجاه التيار المسبب له، مما يؤدي إلى إبطاء القطعة الفلزية وثبات قراءة الميزان. جهاز

مفهوم التوتر السطحي التوتر السطحي (بالإنجليزية: Surface Tension) هي إحدى خصائص سطوح السوائل وتسمح هذه الخاصية للسوائل بمقاومة القوى الخارجية، وذلك بسبب قوى التماسك والتلاصق لجزيئات المواد السائلة فيما بينها، والتي تسمح للماء بالتصرف كغشاء مرن ممتد. لكل مادة توتر سطحي خاص بها، وتختلف فيما بينها، إذ تمتلك السوائل العضوية مثل البنزين والكحول توترًا سطحيًا قليلًا، في حين أن الزئبق يمتلك توتر سطحي أعلى، كما تؤدي الزيادة في درجات الحرارة إلى تقليل قوة الجذب بين جزيئات السائل وبالتالي تقلل من التوتر

تطبيقات على دافعة أرخميدس يوجد عدة تطبيقات على دافعة أرخميدس ومنها ما يلي: تصميم الغواصات السبب الذي يساعد الغواصة على البقاء تحت الماء احتواءها على خزان الصابورة، الذي يستخدم للتحكم في موقع الغواصة وعمقها من على سطح البحر، حيث يدخل الماء إلى داخل خزان الصابورة فتغمر الغواصة فيصبح وزنها أكبر من وزن قوة الطفو، وبالعكس يمكن تطفو الغواصة إلى أعلى عن طريق تقليل الماء من داخل خزان الصابورة فيصبح الوزن أقل من وزن قوة الطفو. تصميم السفن عند بناء السفن يتم استخدام مبدأ أرخميدس حيث يتم تصميم جزء كبير

حساب التغيّر في القيم يمكن تمثيل الزيادة في قيمة معينة على شكل نسبة مئوية عن طريق حساب الفرق بين القيمة بعد الزيادة والقيمة الأصلية ثم قسمة الناتج على القيمة الأصلية، وضرب الناتج الكلي بالعدد 100، ويُمكن تمثيل ذلك من خلال المعادلة الآتية: نسبة الزيادة = ((القيمة بعد الزيادة – القيمة الأصلية) ÷ القيمة الأصلية) *100%. ملاحظة: القيمة السالبة للنسبة السابقة تدل على أن القيمة تتناقص ولا تَزيد. في المقابل يمكن حساب التناقص في قيمة معينة على شكل نسبة مئوية، إما باستخدام نفس معادلة الزيادة في النسبة

تطبيقات على الخلايا الكهروكيميائية تتعدد وسائل إنتاج الطاقة من خلال إجراء التفاعلات الكيميائية ومن بيتها البطاريات الكهربائية التي تخزن الطاقة داخلها أو استعمال الطاقة الكهربائية لتحفيز التفاعلات الكيميائية ويعرف ذلك بالخلايا الكهروكيميائية، وهناك تطبيقات عديدة لاستخدامها منها: الطلاء الكهربائي تهدف هذه العملية إلى طلاء جسم معدني موصل بطبقة من الطلاء باستعمال تيار كهربائي، ويساعد ذلك في حمايته من الخارج من خطر التعرض للتآكل والتلف، بالإضافة لتغيير الشكل الخارجي كاستعماله في صناعة المجوهرات،

تطبيقات على الإعراب والبناء يُعرف الإعراب في اللغة العربية أنّه تغير حركة آخر الكلمة من رفع إلى نصب إلى جر وفق تغير موقعها من الإعراب، أما عن البناء فهو ثبات آخر الكلمة على حركة واحدة في كل أحوالها مهما تغير موقعها من الإعراب. تطبيقات على الإعراب وفيما يأتي أمثلة على المعرب في اللغة العربية نحو ما يُعرب بالحركات الأصلية، مثل جمع التكسير والفعل المضارع: جمع الأطفالُ أنفسهم كي يلعبوا لعبة كرة القدم. فالأطفال ( هي جمع تكسير ) وتُعرب: فاعلًا مرفوعًا للفعل جمع وعلامة رفعه الضم الظاهر على آخره.

تطبيقات حول الإعراب اللفظي الإعراب اللفظي أو الإعراب الظاهر يكون في حالتين هما كالآتي: في الاسم المُتمكن ( الاسم المعرب ). والفعل المضارع الذي لم يتصل بنون النسوة ولا بنون التوكيد. تطبيقات حول الإعراب اللفظي في حالة الرفع ومن التطبيقات حول الإعراب اللفظي في حالة الرفع في الأسماء والأفعال ما يأتي: العَلَمان مرتفعان فوق السارية. الولدُ طويلٌ. ينصب الصيادون شباكهم في الصباح دومًا. قول الشاعر: ذو العَقلِ يَشقى في النَعيمِ بِعَقلِهِ :::وَ أَخو الجَهالَةِ في الشَقاوَةِ يَنعَمُ يجلسُ الطالب في المقعد

تطبيقات الهندسة الوراثية في الإنتاج الحيواني من بعض التطبيقات للهندسة الوراثية في الإنتاج الحيواني ما يأتي: تعديل تكوين الحليب وخصائصه ترتبط بروتينات الحليب بجينات فريدة ومحددة تتحكم في تكوين الحليب، ويمكن التعديل في هذه الجينات للتعديل من خصائصه، ومن بعض التطبيقات على ذلك، إدخال اللاكتوفيرين البشري (lactoferrin) إلى مكونات حليب الأبقار ، حيث أن اللاكتوفيرين مسؤول عن نقل الحديد ومنع نمو البكتيريا، وإدخاله للحليب البقري يكسبه مواد مضادة للبكتيريا، مثل البروتياز (protease) الذي يزيد من مقاومة

تطبيقات المنهج التجريبي يطبق المنهج التجريبي بعدة طرق وذلك بحسب الطرق المتاحة للباحثين التجريبين، ويمكن تقسيمها على النحو الآتي: تطبيق التجارب العمليّة تمتاز التجارب العمليّة بقدرتها على التحكم في المتغيرات الخاصة بمن يقومون بهذه التجارب، ويكون تكرار هذه التجارب أسهل على الباحثين الآخرين. تطبيق التجريب الميدانيّ يتم القيام بتجارب معينة لدراسة مدى استجابة الأشخاص لفعل ما، فعلى سبيل المثال قد يقوم عالم النفس الاجتماعي بدراسة لمعرفة كيف يكون سلوك شخص ما تجاه تجربة معينة كجعل شخص يتظاهر بالإغماء

تطبيقات المعادلات التفاضلية في الهندسة الكهربائية تُعتبر حلول المعادلات التفاضليّة ذات المعامل الثابت من الدرجة الأولى والثانية من المواضيع المهمّة في حل مسائل الهندسة الكهربائيّة ، ويجري توظيفها بالعديد من التطبيقات، وفيما يأتي ذكر أبرزها: الجهد الكهربائي تُعدّ المعادلات التفاضليّة جزءًا مهمًّا من حلّ أيّ تقنيات ومشاكل خاصة في تصميم الجهد الكهربائيّ، حيثُ صُممت شبكة LCK المتسلسلة كدائرة أساسية، وذلك لحلّ معادلة الجهد للدائرة الكهربائيّة، ومقدار القوى المؤثرة داخلها، ومنها: الموجة الجيبيّة

تطبيقات المعادلات التفاضلية الجزئية في الهندسة المدنية تُستخدم المعادلات التفاضلية على نحو واسع في حل مسائل العديد من التخصصات، ومنها الهندسة المدنية ، وعندما تكون المعادلات التفاضلية صعبة الحل، يجري تطبيق طريقة فصل المتغيرات لحل المعادلات التفاضلية الجزئية، وفي إطارها يجري تحويل المعادلات التفاضلية الجزئية إلى مجموعة من المعادلات التفاضلية العادية. فيما يأتي أبرز تطبيقات المعادلات التفاضلية الجزئية في الهندسة المدنية: اهتزازات انحناء الجسور الإنشائية لدراسة اهتزازات انحناء جسر إنشائي ما،

تطبيقات المحاكاة في التعليم لاقت فكرة استخدام أسلوب المحاكاة في العملية التعلمية رواجاً كبيراً في الآونة الأخيرة خصوصاً في ظل تطور البرمجيات التعليمية وأدوات الذكاء الاصطناعي ، ومن تطبيقات استخدام أسلوب المحاكاة في التعليم ما يلي: تعليم الطيران بالمحاكاة صمم هذا التطبيق باستخدام أحداث البرمجيات الحاسوبية وأدوات الذكاء الاصطناعي وذلك من خلال إطلاق تطبيق لمحاكاة عملية الطيران، إذ يُمكن المتعلمون من خوض تجربة قائد الطائرة ضمن واقع افتراضي يحاكي الظروف الحقيقية للملاحة الجوية. وتدريبهم على أساسيات

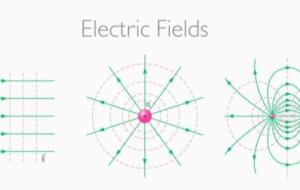
مجالات استخدام المجال الكهربائي وأهم التطبيقات يُعرّف المجال الكهربائي (بالإنجليزية: Electric Field) بأنّه عبارة عن كمية متجهة تتمثل بالفضاء المحيط بجسم مشحون كهربائيًا وتؤثر به الشحنة الكهربائية بقوة كهربائية، إذ تتحرك خطوط المجال الكهربائي مبتعدةً عن الجسم المشحون بشحنة موجبة، أو تتحرك نحوه إذا كان مشحونًا بشحنة سالبة، ورمز المجال الكهربائي هو (E)، كما تعدّ (فولت/متر) وحدة المجال الكهربائي، وتتعدد المجالات والتطبيقات التي يُستخدم فيها المجال الكهربائي ومنها الآتي: تطبيقات المجال الكهربائي في

تطبيقات الكيمياء العضوية في مجال صناعة الأدوية تلعب الكيمياء العضوية دورًا أساسيًّا في الصناعات الدوائية، إذ تعد المركبات العضوية أحد المكونات الرئيسية للأدوية، كما يتم استخدام المعلومات الجديدة المكتشفة بخصوص بالمركبات العضوية في تصنيع أنواع جديدة من الأدوية، وتطوير أصناف الأدوية الموجودة بالفعل، وفيما يأتي تطبيقات على استخدام المركبات العضوية في الصناعات الدوائية: اختراع الأدوية أدى اكتشاف المركبات العضوية إلى إحداث ثورة في مجال صناعة الأدوية، حيث إن العديد من الأدوية يتم تصنيعها من المركبات

تطبيقات الكيمياء التحليلية في الصناعات الدوائية تستخدم الكيمياء التحليلية في الصناعات الدوائية في العديد من التطبيقات، أبرزها: ضمان جودة وكفاءة وسلامة المنتج الدوائي المعروف سابقًا والحديث الذي يتم تطويره. تعتبر عنصرًا هامًا في الصناعات الدوائية، في كل مراحل التصنيع، ما قبل الإنتاج من تحاليل تعتمد للمادة الخام المكونة للدواء، إلى مرحلة خلال وبعد الإنتاج للتأكد من تراكيب الأدوية المصنعة ومطابقتها للمواصفات الدوائية، إلى مرحلة ما بعد البيع ودراسات تحليلية لثباتية الدواء ضمن ظروف خاصة مختلفة.

تطبيقات الكيمياء البيئية تعرف الكيمياء البيئية (بالإنجليزية: Environmental Chemistry) بأنها دراسة تفاعلات المواد الكيميائية والكيميائية العضوية والحيوية التي تحدث في البيئة، كما تشمل الكيمياء البيئية تفاعل المواد الكميائية التي صنعها الإنسان وانتشرت في البيئة، مثل؛ الديوكسينات، والفيوران، ومبيدات الآفات، وثنائي الفينيل متعدد الكلور، وغيرها الكثير. تحتوي جميع مكونات النظم البيئية المختلفة على مجموعة من المواد الكيميائية بتراكيز وكميات مختلفة، وعادةً ما تنتقل هذه المواد بين المكونات المختلفة

الديناميكا الحرارية الديناميكا الحرارية هي دراسة حركة الحرارة، حيث أنه يفسر كل شيء تقريبًا من كيفية انتقال الحرارة أثناء الانصهار والغليان ، إلى ما تعنيه درجة الحرارة، وما إذا كانت الحرارة تتدفق بين الأماكن الباردة والساخنة، كما أنّ للديناميكا الحرارية قوانين مختلفة، ولكننا في هذا المقال سنتطرق بالحديث تحديدًا عن القانون الثالث للديناميكا الحرارية. نص القانون الثالث للديناميكا الحرارية ينص القانون الثالث للديناميكا الحرارية على أنّ القصور الحراري أو الإنتروبيا (بالإنجليزيّة: entropy) ويرمز له

تعريف الديناميكا الحرارية الديناميكا الحرارية هي فرع من فروع الفيزياء، والذي يعنى بدراسة العلاقة بين الحرارة وأشكال الطاقة الأخرى، والذي يصف كيفية تحول الطاقة من طاقة حرارية إلى أشكال أخرى من الطاقة، وكيف تؤثر هذه الطاقة على المادة، حيث تفسر الديناميكا الحرارية الأنظمة التي تتكون من أعداد كبيرة جدًا من الذرات أو الجزيئات، والتي تتفاعل معاً بطرق معقدة. تطبيقات الديناميكا الحرارية يوجد العديد من التطبيقات للديناميكا الحرارية في الحياة، منها: وفقًا للقانون الثاني للديناميكا الحرارية ، تتدفق

تطبيقات التفاضل والتكامل في الهندسة يستخدم بعض المهندسين التفاضل والتكامل في أعمالهم اليومية والبعض الآخر في أجهزة الحاسوب التي تكون قائمة على حساب التفاضل والتكامل الذي يقوم بتبسيط التصميم الهندسي، وفي ما يلي بعض تطبيقات التفاضل والتكامل في الهندسة: في الهندسة المعمارية يتم استخدام التكامل في الهندسة المعمارية (بالإنجليزية: Architecture) وذلك في ما يلي: لتحديد كمية المواد اللازمة لإنشاء هيكل يحتوي على شكل منحني مثل قبة فوق ساحة رياضية ويتم استخدام التفاضل والتكامل لقياس وزن هذا الهيكل. يستخدم

تطبيقات الاستنتاج الرياضي الاستنتاج الرياضي هي مجموعة بيانات رياضية يتم تجميعها لإنجاح عمليات حياتية كثيرة، وتوجد عدة تطبيقات لهذه الاستنتاجات في الحياة العملية، وأبرزها تطوير تطبيقات تقنيات الذكاء الاصطناعي ، والتكوين النظري الآلي، وبعض الدورات التدريبية الخاصة بالاستنتاج الرياضي. تطوير تطبيقات تقنيات الذكاء الاصطناعي تشمل تطبيقات الاستنتاج الرياضي تطوير تطبيقات تقنيات الذكاء الاصطناعي، والتي تقود لتطوير أنظمة الجبر الحاسوبية، ومثبتات النظريات الحاسوبية الحديثة؛ بدلاً من تطوير أنظمة التعلم