شرح جمع وطرح الكسور مع الأمثلة
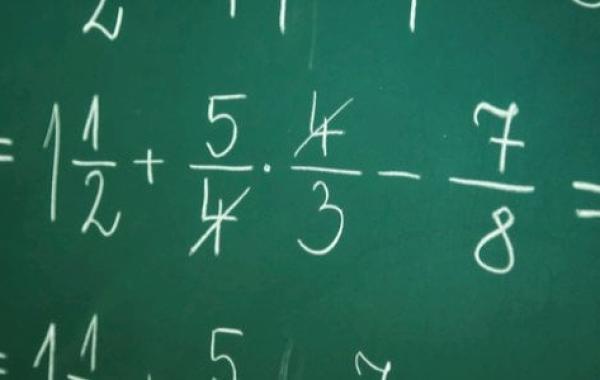
كيفية جمع الكسور
الكسور هي عدّة أجزاء متساوية من الكل؛ أي إذا قسمنا الكل إلى أجزاء متساوية يكون كل جزء عبارة عن جزء من الكل ويُسمى كسرًا، ويُكتب الكسر ببسط ومقام؛ حيث يُعبر البسط عن عدد الجزء الذي اُخذ من الكل، ويُعبر المقام عن الكل أو العدد الإجمالي، ويكون كل من البسط والمقام أعداد صحيحة، والمقام لا يساوي صفراً، والكسر عدد نسبي وبالتالي هو عدد حقيقي .
ويجدر بالذكر أنّ هناك نوع آخر من الكسور؛ وهو الكسر المختلط -العدد الكسري- والذي يتكوّن من كسر عادي وعدد صحيح، وعند جمع وطرح الكسور المختلطة تُحوّل إلى كسور عاديّة ليبسط حلها، ويُمكن تحويلها بالخطوات التالية:
مثال: حوّل (2/3) 3 إلى كسر عادي.
- نضرب المقام (3) في العدد الصحيح (3)، ثم نجمع الناتج إلى البسط (2)، ثم نضع الناتج على المقام نفسه.
- نضرب المقام في العدد الصحيح: 3×3=9.
- نجمع الناتج إلى البسط: 2 9= 11.
- نضع الناتج على المقام نفسه: 11/3.
وفيما يلي شرح لكيفية جمع الكسور:
جمع الكسور ذات المقامات المتساوية
ولجمع الكسور ذات المقامات المتساوية يُمكن اتّباع الخطوات التالية:
على سبيل المثال جمع: 3/6 1/6
- نجمع البسط مع البسط ونضع الناتج في البسط: 3 1=4.
- نُبقي المقام كما هو؛ لذا نضع ناتج جمع البسط فوق المقام، الناتج: 4/6.
- نُبسّط ناتج الكسر إذا لزم الأمر.
- نُلاحظ أنّ العددان 4 و6 يقبلان القسمة على العدد 2، لذا نقسم البسط والمقام على 2 لتبسيطه قدر الإمكان.
- (2÷6)/ (2÷4)= 2/3.
- وبالتالي يكون الناتج: 1/6 3/6= 2/3.
جمع الكسور ذات المقامات المختلفة
وفيما يأتي خطوات لجمع المقامات المختلفة في الكسور:
على سبيل المثال: 1/2 (1/6) 2
- نوحد المقامات، وذلك بإيجاد المضاعف المشترك الأصغر.
- نُلاحظ في المثال أنّ لدينا كسر مختلط؛ لذا قبل توحيد المقامات نحول الكسر المختلط إلى كسر عادي.
- (6×2) 1= 1 12= 13، إذا يُصبح الكسر: 13/6.
- تُصبح المسألة: 1/2 13/6
- نوحد المقامات، ونُلاحظ أنّ العدد 6 من مضاعفات العدد 2، إذًا نضرب بسط ومقام العدد 1/2 بالرقم 3 ليُصبح المقام 6.
- (3×2)/ (3×1)= 3/6= 1/2.
- تُصبح المسألة بعد توحيد المقامات: 3/6 13/6
- نجمع البسط مع البسط والمقام نفسه: 6/(13 3)= 16/6.
- نُبسط الناتج، نُلاحظ أن الرقمان يقبلان القسمة على الرقم 2، لذا نقسم البسط والمقام على العدد 2.
- (2÷6)/ (2÷16)= 8/3
- وبالتالي يكون الناتج: 1/2 (1/6) 2 = 8/3
أمثلة متنوعة على جمع الكسور
نورد هنا عدة أمثلة على جمع الكسور ذات المقامات المتساوية، والمختلفة، والمختلطة على النحو الآتي:
أمثلة متنوعة على جمع الكسور ذات المقامات المتساوية
فيما يأتي أمثلة تطبيقية على جمع الكسور ذات المقامات المتساوية:
أوجد ناتج جمع المعادلة التالية: 2/7 1/7
- نجمع البسط مع البسط ونضع الناتج في البسط، ونُبقي المقام كما هو.
- 7 / (1 2)= 3/7
- وبالتالي يكون الناتج: 2/7 1/7= 3/7
أوجد ناتج المعادلة التالية: 13/10 7/10
- نجمع البسط مع البسط ونضع الناتج في البسط، ونُبقي المقام كما هو.
- 10/ (7 13)= 20/10.
- نبسط الناتج ليُصبح 2/1.
- وبالتالي يكون الناتج: 13/10 7/10= 2.
أمثلة متنوعة على جمع الكسور ذات المقامات المختلفة
وفيما يأتي أمثلة تطبيقية على جمع الكسور ذات المقامات المختلفة:
أوجد ناتج المعادلة التالية: 7/15 4/5
- نوحد المقامات، نجد أنّ العدد 15 من مضاعفات العدد 5؛ إذًا نضرب بسط ومقام العدد 4/5 بالعدد 3 ليصبح المقام يساوي 15.
- (3×5) / (3×4) =12/15= 4/5
- تُصبح المسألة بعد توحيد المقامات: 7/15 12/15
- نجمع البسط مع البسط والمقام نفسه: 15/ (7 12)= 19/15.
- وبالتالي يكون الناتج: 7/15 4/5= 19/15.
أوجد ناتج المعادلة التالية: 7/2 3/10
- نوحد المقامات، نجد أنّ العدد 10 من مضاعفات العدد 2؛ إذًا نضرب بسط ومقام العدد 7/2 بالعدد 5 ليصبح المقام يساوي 10.
- (5×2)/ (5×7)= 35/10= 7/2
- تُصبح المسألة بعد توحيد المقامات: 35/10 3/10
- نجمع البسط مع البسط والمقام نفسه: 10/(35 3)= 38/10.
- نُبسط الناتج نُلاحظ أن العددان يقبلان القسمة على 2، نقسم البسط والمقام على 2.
- (2÷10)/ (2÷38)= 19/5.
- وبالتالي يكون الناتج: 7/2 3/10= 19/5
أمثلة متنوعة على جمع الكسور المختلطة.
وفيما يأتي أمثلة تطبيقية على جمع الكسور ذات المقامات المختلفة:
أوجد ناتج المعادلة التالية: (3/2) 3 (4/2) 2
- نحول الكسر المختلط إلى كسر عادي.
- 2/(4 4) =2/(4 (2×2))= (4/2) 2= 8/2
- 2/(6 3) =2/(3 (3×2))= (3/2) 3= 9/2
- تُصبح المعادلة: 9/2 8/2
- المقامات موحدة:
- 2 / (8 9)= 17/2.
- وبالتالي يكون الناتج: (3/2) 3 (4/2) 2= 17/2.
أوجد ناتج المعادلة التالية: (1/4) 2 (5/4) 2
- نحول الكسر المختلط إلى كسر عادي.
- 4/(8 5) =4/(5 (2×4)) =13/4= (5/4) 2
- 4/(8 1) =4/(1 (2×4)) =9/4= (1/4) 2
- تُصبح المعادلة: 9/4 13/4
- المقامات موحدة: 4/ (13 9)= 22/4.
- نُبسط الناتج بقسمة البسط والمقام على 2.
- (2÷4) / (2÷22)= 11/2.
- وبالتالي يكون الناتج: (1/4) 2 (5/4) 2= 11/2.
من المهم مذاكرة الرياضيات جيداً، وحل العديد من المسائل لفهمه، ومن أهم الأمور التي يجب مذاكرتها هي الكسور؛ إذ إنّ الكسر هو عدد يُكتب بقسمة بسط على مقام، وهما عددان صحيحان والمقام لا يساوي صفر، وعلاقة البسط مع المقام هي علاقة جزء أو عدّة أجزاء متساوية مع الكل، كما يُمكن كتابة الكسر على صورة كسر مختلط مكوّن من كسر عادي وكسر صحيح، وتُجمع الكسور من خلال توحيد المقامات، ثم جمع البسط لكل عدد وترك المقام كما هو.
كيفية طرح الكسور
عملية الطرح هي عملية تُستخدم لإيجاد الفرق بين الأرقام ويُرمز لها بالرمز (-)، والطرح عكس عملية الجمع ، وفيما يلي شرح كيفية جمع الكسور:
طرح الكسور ذات المقامات المتساوية
ولطرح الكسور ذات المقامات المتساوية يُمكن اتباع الخطوات التالية:
على سبيل المثال: 2/23-12/23
- نطرح البسط مع البسط ونضع الناتج في البسط (12-2).
- نُبقي المقام كما هو، لذا نضع ناتج جمع البسط فوق المقام (23).
- نُبسّط ناتج الكسر إذا لزم الأمر.
- 23/ (12-2)= 10/23.
- وبالتالي يكون الناتج:2/23 - 12/23= 10/23
طرح الكسور ذات المقامات المختلفة
وفيما يلي خطوات لطرح المقامات المختلفة في الكسور:
على سبيل المثال: 5/3 - 17/9
- لتوحيد المقامات في عملية الطرح نجد المضاعف المشترك الأصغر.
- نطرح البسط من البسط ونضع الناتج في البسط والمقام نفسه، ثم نُبسّط الناتج إذا لزم الأمر.
- نوحد المقامات، نُلاحظ أنّ العدد 9 من مضاعفات العدد 3، إذًا نضرب بسط ومقام العدد 5/3 بالرقم 3 ليصبح المقام 9.
- (3×3)/ (3×5)= 15/9.
- تُصبح المسألة بعد توحيد المقامات: 15/9 - 17/9
- نطرح البسط من البسط والمقام نفسه: 9/ (15-17)= 2/9.
- وبالتالي يكون الناتج: 5/3 - 17/9= 2/9.
أمثلة متنوعة على طرح الكسور
نورد هنا عدداً من الأمثلة على طرح الكسور ذات المقامات المتساوية، والمختلفة، والمختلطة كما يأتي:
أمثلة متنوعة على طرح الكسور ذات المقامات المتساوية
فيما يأتي أمثلة تطبيقية على طرح الكسور ذات المقامات المتساوية:
أوجد ناتج طرح المعادلة التالية: 7/11-10/11
- نطرح البسط من البسط ونضع الناتج في البسط، ونُبقي المقام كما هو.
- 11/ (10-7)= 3/11.
- وبالتالي يكون الناتج: 7/11-10/11= 3/11.
أوجد ناتج طرح المعادلة التالية: 141/100-211/100
- نطرح البسط من البسط ونضع الناتج في البسط، ونُبقي المقام كما هو.
- 100/ (211-141)= 70/100 = 7/10.
- وبالتالي يكون الناتج: 141/100- 211/100= 7/10.
أمثلة متنوعة على طرح الكسور ذات المقامات المختلفة
فيما يأتي أمثلة تطبيقية على طرح الكسور ذات المقامات المختلفة:
أوجد ناتج المعادلة التالية: 7/3 - 33/12
- نوحد المقامات، نجد أنّ العدد 12 من مضاعفات العدد 3، إذًا نضرب بسط ومقام العدد 7/3 بالعدد 4 ليصبح المقام يساوي 12.
- (4×3) / (4×7)=28/12= 7/3.
- تُصبح المسألة بعد توحيد المقامات: 28/12 - 33/12.
- نطرح البسط من البسط والمقام نفسه: 12/ (28-33)= 5/12.
- وبالتالي يكون الناتج: 7/3 - 33/12= 5/12.
أوجد ناتج المعادلة التالية: 1/5 - 3/6
- نوحد المقامات، نجد أنّ المضاعف المشترك الأصغر بين العددين 5 و 6 هو 30، نضرب بسط ومقام العدد 1/5 بالعدد 6، ونضرب بسط ومقام العدد 3/6 بالعدد 5.
- (5×6)/(5×3) =15/30= 3/6
- (6×5)/(6×1)= 6/30= 1/5
- تُصبح المسألة بعد توحيد المقامات: 6/30 - 15/30
- نطرح البسط من البسط والمقام نفسه: 9/30 = 30/ (6-15)
- نبسط الناتج بقسمة البسط والمقام على 3.
- (3÷30)/(3÷9)= 3/10 =
- وبالتالي يكون الناتج: 1/5-3/6= 3/10.
أمثلة متنوعة على طرح الكسور المختلطة.
فيما يأتي أمثلة تطبيقية على طرح الكسور ذات المقامات المختلطة:
أوجد ناتج المعادلة التالية: (4/2) 2 - (3/2) 3
- نحول الكسر المختلط إلى كسر عادي.
- 2/(6 3) =2/(3 (3×2)) =9/2 = (3/2) 3
- 2/(4 4) =2/(4 (2×2)) =8/2 = (4/2) 2
- تُصبح المعادلة: 8/2 9/2
- المقامات موحدة، نطرح البسط من البسط ونضع الناتج فوق المقام نفسه.
- 2/ (9-8)= 1/2.
- وبالتالي يكون الناتج: (4/2) 2 - (3/2) 3= 1/2.
أوجد ناتج المعادلة التالية: (1/2) 2 - (12/4) 2
- نحول الكسر المختلط إلى كسر عادي.
- 4/(8 12) =4/ (12 (2×4)) =20/4 = (12/4) 2
- 2/(4 1) =2/(1 (2×2)) =5/2 = (1/2) 2
- تُصبح المعادلة: 5/2 - 13/4
- نوحد المقامات بضرب بسط ومقام الكسر 5/2 بالعدد 2.
- (2×2)/ (2×5)= 10/4.
- تُصبح المعادلة بعد توحيد المقامات: 10/4 - 20/4
- نطرح البسط من البسط ونضع الناتج فوق المقام نفسه.
- 4/ (20-10)= 10/4.
- نُبسط الناتج بقسمة البسط والمقام على 2.
- (2÷4)/ (2÷10)= 5/2.
- وبالتالي: (1/2) 2 - (12/4) 2= 5/2.
يُرمز لعملية الطرح بالرمز (-)، وهي عكس عملية الجمع وتُستخدم لإيجاد الفرق بين عددين، ويُمكن طرح الكسور بتوحيد المقامات من خلال إيجاد المضاعف المشترك الأصغر، ثم طرح البسط من البسط مع ترك المقام كما هو.







