خواص القيمة المطلقة
خصائص القيمة المطلقة
هناك العديد من خصائص القيمة المطلقة، ومنها ما يلي:
- |أ|≥0؛ أي أن القيمة المطلقة للعدد أ لا يمكن لها أن تكون أقل من الصفر؛ حيث أ أي عدد حقيقي.
- |أ|= (أ)√؛ حيث يساوي جذر العدد عدداً موجباً أو مساوياً للصفر في الأعداد الحقيقية.
- |أ×ب|=|أ|×|ب|، وهذا يعني أن حاصل ضرب القيمة المطلقة للعدد أ بالقيمة المطلقة للعدد ب يساوي القيمة المُطلقة لحاصل ضرب العددين أ و ب.
- |أ|=|-أ|, حيث يمتلك العدد وسالبه القيمة المطلقة ذاتها.
- |أ-ب|=|ب-أ|؛ حيث (أ-ب) ≠ (ب-أ)، بينما القيمة المطلقة لهما متساوية.
- |أ|=|ب|، فقط إذا كانت أ=ب، أو أ=-ب.
- |أ|=|أ |، حيث ن= عدد صحيح موجب.
- |أ|/|ب|=|أ/ب|، حيث ب لا تساوي صفر.
- |أ±ب|≤|أ| |ب|, وتعني أن القيمة المطلقة لمجموع قيمة العددين أ, ب أقل دائماً أو مساوية لناتج جمع أو طرح القيمة المطلقة للعدد أ مع القيمة المطلقة للعدد ب.
ملاحظة: يمثل المتغيران أ، ب في الخصائص السابقة أي عددين حقيقيين.
تعريف القيمة المطلقة
يمكن تعريف القيمة المطلقة (بالإنجليزية: Absolute Value) بأنّها المسافة التي يبعدها العدد الحقيقي بغض النظر عن إشارته عن الصفر على خط الأعداد، فالعدد 6 يبعد عن الصفر بمقدار 6، وكذلك الأمر بالنسبة للعدد (-6)، وهي تُعنى بقيمة العدد دون النظر إلى إشارته، وتُستخدم عادة عند التكلم عن المسافات، لعدم وجود مسافات سالبة في الواقع والحياة.
كيفية كتابة القيمة المطلقة
تُكتب القيمة المطلقة للعدد س مثلاً باستخدام الرمز الآتي: |س|؛ فمثلاً يمكن التعبير عن القيمة المطلقة للعدد (5) على شكل |5| = 5، وكذلك الأمر بالنسبة للعدد (-5): |5-|=5، وهي تعني عملياً إزالة الإشارة السالبة الموجودة أمام العدد، والتفكير في جميع الأعداد على أنها موجبة دائماً أو مساوية للصفر فقط.
اقتران القيمة المطلقة
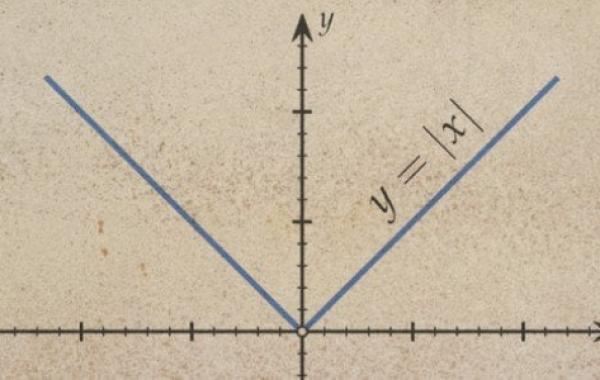
يعبّر عن اقتران القيمة المطلقة بالصيغة الآتية: ق(س)=|س|، وهو يحوّل قيمة س إلى القيمة الموجبة دائماً؛ فمثلاً ق(4-)=|4-|=4، وياخذ هذا الاقتران عند تمثيله بياناً شكل حرف (V)، ويمتاز بالمميزات الآتية:
- مجاله هو جميع الأعداد الحقيقية .
- مداه هو جميع الأعداد الحقيقية التي تساوي أو تزيد عن الصفر.
- رسمه البياني يقع بالكامل فوق محور السينات.
- رسمه البياني متماثل بالنسبة لمحور الصادات.
أمثلة متنوعة على القيمة المطلقة
وفيما يأتي أمثلة متنوعة على القيمة المطلقة:
المثال الأول: ما هو ناتج كل مما يلي:
| السؤال | الحل |
| |3.5|-|2.5-| | |3.5| - |2.5-| = 3.5 - 2.5=1 |
| |5×6| | |5×6|=|30|=30 |
| |2×(2/3 - 0.5)| | |2×(2/3 - 0.5)| = |2×(1/6)| = |1/3| = 1/3 |
| |12-|- | |12-|-= 12- |
| |²(2-)|- | |²(2-)|- = |4|- = 4- |
| |³(-3) 5| | |³(-3) 5| = |27 5-| =|22-| = 22 |
المثال الثاني: احسب قيمة س في المسألة: |س 2|=5؟
الحل:
- س 2=5±، ومنه:
- س 2=5، ومنها س=3.
- س 2=5- ، ومنها س=7-.
المثال الثالث: احسب مدى س في المسألة: |س| [٦]
الحل:
- يمكن كتابة هذه المسألة على شكل: س
- س-3؛ أي أن -3
المثال الرابع: احسب مدى س في المسألة: |3س-6| ≤ 12.
الحل:
- يمكن كتابة هذه المسألة على شكل: (3س-6)≤ 12±، وبالتالي: 3س-6 ≤ 12، أو 3س-6 ≤ 12-، ومنه:
- 3س-6≤ 12، تصبح بعد جعل س على طرف لوحدها: س≤ 6.
- 3س-6 ≤ 12-، تصبح بعد جعل س على طرف لوحدها: 2- ≤ س .
- وبالتالي: 2- ≤ س ≤ 6
المثال الخامس: احسب قيمة س في المسألة: |س-2| |س-3| = 1.
الحل:
- يمكن كتابة هذه المسألة على شكل: ±(س-2)±(س-3) = 1، وبالتالي هناك عدة حالات على الشكل الآتي:
- س-2 س-3= 1، وبالتالي: 2س-5 =1، ومنه: س= 3.
- -س 2 - س 3 = 1، وبالتالي: -2س 5=1، ومنه: س = 2.
- س-2- س 3= 1، وهذه المسألة لا حلول لها لأن س تلغي بعضها.
- -س 2 س-3= 1، وهذه المسألة لا حلول لها لأن س تلغي بعضها.
- حلول هذه المسألة هي: س= 2،3.
المثال السادس: احسب قيمة س في المسألة: |3س-2| = |5س 4|.
الحل:
- يمكن كتابة هذه المسألة على شكل: (3س-2) = ±(5س 4)، وبالتالي هناك عدة حالات على الشكل الآتي:
- 3س-2 = 5س 4، ومنه: س= 3-.
- 3س-2 = -5س-4، ومنه: س= 1/4-.
- حلول هذه المسألة هي: س=1/4-، 3-.
المثال السابع: إذا كانت قيمة س=2، جد قيمة ما يلي: |-4س 3| |3س-14|.
الحل: بتعويض قيمة س ينتج أن: |(-4×2) 3|×|(3×2)-14| = |5-|×|8-| = 5×8 = 40.
المثال الثامن: إذا كان: |2أ-3| = 5، |3-4ب| = 11، جد قيمة |ب-أ|، علماً أن أ، ب أعداد سالبة.
الحل:
- |2أ-3| = 5، ومنه: 2أ-3 = 5±، وبالتالي: 2أ-3 = 5، وبحلها ينتج أن أ=4، أو 2أ-3 = 5-، وبحلها ينتج أن: أ=1-، وهي القيمة المطلوبة.
- |3-4ب| = 11، ومنه: 3-4ب = 11±، وبالتالي: 3-4ب = 11، وبحلها ينتج أن: ب= 2-، وهي القيمة المطلوبة، أو 3-4ب = 11-، وبحلها ينتج أن: ب=2.
- قيمة |ب-أ| هي: |-2-(-1)| = |1-| =1.
تُكتب القيمة المطلقة للعدد س مثلاً باستخدام الرمز الآتي: |س|، إذ يعبّر عن اقتران القيمة المطلقة بالصيغة الآتية: ق(س)=|س|، وهو يحوّل قيمة س إلى القيمة الموجبة دائماً، وللقيمة المطلقة العديد من الخصائص وأهمها؛ أنها لا يمكن أن تكون أقل من الصفر، وحاصل ضرب القيمة المطلقة للعدد أ بالقيمة المطلقة للعدد ب يساوي القيمة المُطلقة لحاصل ضرب العددين أ و ب، والقيمة المطلقة لمجموع قيمة العددين أ, ب أقل دائماً أو مساوية لناتج جمع أو طرح القيمة المطلقة للعدد أ مع القيمة المطلقة للعدد ب، وغيرها العديد.







