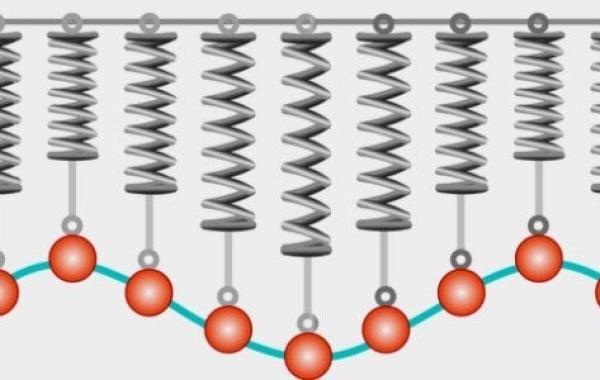
قانون هوك
في القرن السابع عشر نشر الفيزيائيّ البريطانيّ روبرت هوك (بالإنجليزيّة: Robert Hooke) نتائج دراسته للنوابض، وما توصّل إليه هو أنّ القوة اللازمة لجعل النابض يستطيل أو ينضغط تتناسب مع مقدار هذا الانضغاط أو هذه الاستطالة، أو بكلماتٍ أخرى: إنّ القوة تتناسب مع مقدار إزاحة النابض عن نقطة الاتزان.
ويُعبَّر عن قانون هوك رياضيّاً، بهذا القانون:
ق= - ض × س
حيث إنّ:
- ق: هي القوة المؤثرة على النابض.
- س: هي مقدار الإزاحة عن نقطة اتّزان النابض، أي أنّها مقدار الاستطالة أو الانضغاط.
- ض: هو ثابت النابض؛ وهو يدلّ على مدى صلابة النابض.
يُعدّ قانون هوك أوّل مثال كلاسيكيّ يُوضّح المرونة؛ حيث إنّ المرونة هي خاصيّة في الأجسام، تُمكّنها من العودة إلى شكلها الأصليّ بعد زوال القوة المؤثرة عليها.
وقد توصّل العالم روبرت هوك إلى هذا القانون بعدما لاحظ الرسم البياني لمنحنى الضغط (بالإنجليزيّة: Stress) والإجهاد (بالإنجليزيّة: Strain)، بحيث يسلك سلوكاً خطياً إلى حدٍّ مُعيّن، وضمن المنطقة التي يكون فيها سلوك المادة خطياً فإنّ مرونة المادة تكون واضحةً ولا يحدث تشوّه لها.
تطبيقات على قانون هوك
لا شك بأن قانون هوك ذو أهمية عملية كبيرة، فهنالك العديد من التطبيقات اليومية عليه، ومن أهمها:
يحتوي قلم السحب على نوابض أو زنبركات متصلة بأعلى وأسفل خرطوشة الحبر، بالإضافة إلى وجود أنبوب بلاستيكي مثبت داخل القلم، وتعمل الزنبركات حسب مبدأ قانون هوك على إخراج خرطوشة الحبر أو إدخالها إلى الأنبوب البلاستيكي حسب الحاجة.
- الارتداد الحاصل في لعبة المسدس الخاصة بالأطفال
تحتوي لعبه المسدس على زنبرك متصل بآخر المسدس، وعند إطلاق رصاصة اللعبة يؤدي الزنبرك وظيفته بإعادة التلقيم التلقائي للرصاص، ويمثل هذا الارتداد تطبيقًا مباشرًا على قانون هوك.
عند نفخ البالون بالهواء يتمدد، وعند إفراغه من الهواء يتقلص، ويعتمد كل من تمدد البالون وتقلصه على القوة التي تضغط الهواء فيه، لذا فهو يعد تطبيقًا آخر على قانون هوك.
- عجلة التوازن الموجودة في الساعة
تتمتع عجلة التوازن الخاصة بالساعة بحركة دائمة بفضل النابض أو الزنبرك، وتساعد العجلة إبرة الساعة على الحركة دوريًا وبمعدل ثابت، ويوصل الزنبرك بمركز هذه العجلة عند أحد أطرافه ويكون الطرف الآخر له ثابتًا، وبسبب استخدام الزنبرك تعد هذه العجلة من التطبيقات البارزة على قانون هوك.
يحتوي هذا الميزان على قرص متحرك ومتدرج بالإضافة إلى مؤشر يعرض وزن الجسم، ويتصل القرص برافعة، والتي تتصل بدورها بزنبرك يدفعها على الحركة وفقًا لوزن الجسم الموضوع عليه، وهذا يمثل تطبيقًا عمليًا على قانون هوك.
أمثلة حسابية على قانون هوك
مثال (1): احسب القوّة المؤثّرة على نابض إذا علمت أنّ مقدار التَّغير في طوله 4 سم، ومعامل المرونة أو ثابت القوة مقداره 625 نيوتن/م؟
الحل: يُرمَز لمقدار الإزاحة بالرمز س، إلا أنّه هنا بوحدة السنتيمتر، لذا يتمّ تحويله إلى وحدة المتر، وذلك بقسمته على 100:
وبتعويض قيمة كلٍّ من الإزاحة ومعامل المرونة في قانون هوك:
- ق=-ض×س
- ق=-625×0.04
- ق=-25 نيوتن.
مثال (2): شخص كتلته 75كغ، يقف على نابض قابل للانضغاط، وقيمة ثابت هذا النابض هي 5000 نيوتن/م، احسب مقدار انضغاط هذا النابض.
الحل: المطلوب في هذا المثال هو إيجاد مقدار الإزاحة، ويُمكن إيجادها من خلال تعويض قيمة كلٍّ من القوة ومعامل المرونة في قانون هوك، إلا أنّ مقدار القوّة المؤثّرة على النابض مجهول، ولكن يُمكن إيجاده من كتلة الشخص الواقف على النابض، وذلك بضرب قيمة الكتلة بقيمة تسارع الجاذبية الأرضية، وذلك كما يأتي:
- ق= كتلة الشخص×تسارع الجاذبية الأرضية
- ق=75×9.81
- ق=735.75 نيوتن
بتعويض القيم في قانون هوك، وبقسمة الطرفين على معامل المرونة:
- ق=-ض×س
- س=-ق/ض
- بالتعويض في قانون هوك:
- س=-5000/735.75
- س=-0.147م؛ هذا يعني أنّ النابض سينضغط مسافة 14.7سم، والإشارة السالبة تعني أنّ طول النابض سوف يقلّ 14.7سم.
مثال (3): إذا شُد زنبرك بمقدار 10 سم، وكان ثابت النابص يساوي 2 نيوتن / سم، فكم قيمة القوة المطبقة عليه؟
الحل:
- يجب دائمًا التأكد من تطابق الوحدات على طرفي القانون قبل البدء بالحل:
- ق (نيوتن) = ض (نيوتن /سم) × س (سم)؛ التطابق في الوحدات حاصل.
-
- ق = - 2 × 10
مثال (4): جد قيمة ثابت قوة الزنبرك لزنبرك يمتد بمقدار إزاحة بالغة 0.8 م بعد تطبيق قوة مقدارها 100 نيوتن عليه.
الحل:
- باستخدام القانون: ض= - ق / س
- ض = - 100 نيوتن / 0.8 م
- ض = - 125 نيوتن / م.
مثال (5): إذا كان هناك 50 جول من الطاقة الكامنة المرنة موجودة في زنبرك تم ضغطه بمقدار 0.5 متر من موضع اتزانه. فما هي قيمة ثابت هذا الزنبرك؟
الحل:
- يمكن إيجاد طاقة الوضع الخاصة بالزنبرك من خلال قسمة ثابت الزنبرك على 2 وضرب الناتج بمربع الإزاحة التي تحركها، وفق القانون الآتي: ط و للزنبرك = 0.5 × ض × س
- ومنه يمكن إيجاد ثابت الزنبرك أو النابض كما يلي: ثابت النابض (ض)= (2× الطاقة الكامنة أو الوضع)/ س
- ض = (2×50)/ (0.5)
- ض = 400 نيوتن / م.
أنواع تشوّه المادّة حسب قانون هوك
عند تطبيق قوّةٍ ما على مادّةٍ ما، فإنّ هذه المادّة ستستجيب لهذه القوة؛ فتنضغط أو تزداد طولاً (استطالةً)، وتُعرَف هذه القوة التي تؤثر على مادّةٍ ما مُسبّبةً تغيراً في طولها بالضغط، أمّا استجابة المادّة لهذه القوة؛ سواءً أكانت زيادةً في الطول، أم نقصاناً فيه، فإنّها تُعرَف بالجهد.
والجهد هو النسبة بين التغير الحاصل في طول المادة وطولها الأصليّ، تختلف استجابة المواد للقوة المؤثرة عليها باختلاف المادة التي تُطبَّق عليها القوة، ويرجع هذا الاختلاف في الاستجابة بين مادّة وأخرى إلى اختلاف البنية الجزيئية باختلاف المادّة، ويتناسب مقدار استجابة المادة مع قوة الروابط الكيميائية بين جزيئاتها، ونوع هذه الروابط وهذا يشبه ما عبّر عنه قانون هوك.
بعد إزالة القوة المؤثرة عن هذه المادّة، فإنّ التشوّه الحاصل لها يعتمد على مقدار ابتعاد جزيئات المادة عن بعضها البعض، والتشوه سيكون أحد هذين النوعين:
(بالإنجليزيّة: Elastic Deformation) عند زوال القوة المؤثرة، فإنّ الجسم سيعود إلى شكله الأصلي وأبعاده الأصليّة قبل أن تؤثر القوة عليه، وهذا يعني أنّ التشوه الحاصل هنا هو تشوّه مؤقّت وغير دائم.
(بالإنجليزيّة: Plastic Deformation) لحدوث هذا التشوه فإنّه يلزم التأثير بقوة كبيرة جداً؛ بحيث لا يعود الجسم إلى شكله الأصلي وستتغيّر أبعاده عندما تزول هذه القوة، وهذا يعني أنّ التشوه الحاصل هنا هو تشوّه دائم ولن يزول.
يعد قانون هوك أول مثال تم شرح خاصية المرونة للأجسام باستخدامه، إذا نص القانون على أن القوة المبذولة لجعل الزنبرك يتمدد أو ينقبض يتناسب مع مقدار هذا الانقباض أو التمدد.
ويمكن ملاحظة العديد من التطبيقات اليومية على قانون هوك مثل: نفخ البالون، والميزان الأرضي، وأقلام السحب، وألعاب المسدسات للأطفال، وغيرها الكثير من التطبيقات.
