بحث عن قوانين الغازات
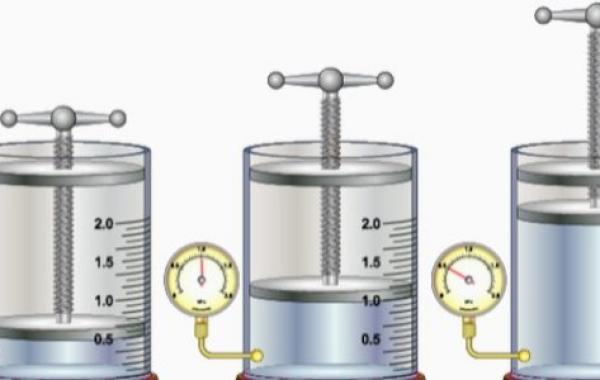
قوانين الغازات
طوّر العلماء قوانين الغازات في نهاية القرن 18، وهي قوانين تصف سلوك الغازات من خلال بعض العوامل، مثل:
- الحجم الذي يشغله الغاز باللتر.
- الضغط الذي يمارسه الغاز على جدران الوعاء الموضوع فيه.
- درجة الحرارة المطلقة للغاز بالكلفن .
- كمية المادة الغازية، أو عدد مولات الغاز.
وفيما يأتي ذكر لأهم قوانين الغازات:
قانون الغاز المثالي
ينص قانون الغاز المثالي (بالإنجليزية: The Ideal Gas Law) على أنّ الغاز المثالي هو الغاز الذي تكون فيه جميع التصادمات بين الذرات أو الجزيئات مرنة تمامًا، ولا توجد أي قوى رابطة بين جزيئاتها، إذ يمكن تخيُّلها على أنّها مجموعة من الجزيئات أو الأجسام الصلبة التي تتصادم بشكل عشوائي دون حدوث أي تفاعل فيما بينها.
يربط قانون الغاز المثالي جميع العوامل التي من الممكن أن تؤثر على الغاز من خلال الصيغة الرياضية الآتية:
P × v =n × R × T
حيث إنّ:
- P: الضغط، ويقاس بوحدة ضغط جوي.
- V: حجم الغاز، بوحدة اللتر.
- n: عدد المولات في الغاز، وتقاس بوحدة المول.
- R: ثابت الغاز العام، وهو: 0.0821 (لتر× ضغط جوي) / (مول×كلفن).
- T: درجة حرارة الغاز، وتقاس بالكلفن.
قانون بويل
يشرح قانون بويل (بالإنجليزية: Boyle's Law) العلاقة بين ضغط وتمدد الغاز عند درجة حرارة ثابتة، حيث صاغ العالم روبرت بويل هذه العلاقة والتي تنص على أنّ قيمة الضغط لكمية معينة من الغاز تتناسب عكسيًا مع حجم هذا الغاز عند درجة حرارة ثابتة.
يمكن تمثيل القانون الذي يوضح قانون بويل من خلال الصيغة الرياضية الآتية:
p × V = c
وفي حال مقارنة غازين معاً، تُستخدم هذه العلاقة:
p1 × V1 = p2 × V2
حيث تشير الرموز إلى ما يأتي:
- V: حجم الغاز، ويقاس بوحدة اللتر.
- p: ضغط الغاز، ويقاس بوحدة ضغط جوي.
- C: ثابت يعتمد على نوع الغاز ودرجة الحرارة، ووحدته باسكال.م^3.
قانون شارل
يربط قانون شارل بين حجم الغاز المثالي ودرجة حرارته عند بقاء العوامل الأخرى ثابتة، وينص قانون شارل على أنّ حجم الغاز المثالي يتناسب طرديًا مع درجة حرارته المطلقة عند ثبوت الضغط ، واكتُشفت هذه العلاقة عام 1787 م من قِبل العالم جاك شارل، و يوجد العديد من التطبيقات الحياتية من حولنا على قانون شارل .
يمكن تمثيل القانون بالصيغة الرياضية الآتية:
V/T = k
وفي حال وجود نوعين من الغاز للمقارنة بينهما، أو لحل المسائل المتعلقة بنفس الغاز ذو الحجم أو درجة الحرارة المتغيرين تُستخدم العلاقة الآتية:
V1/ T1 = V2/ T2
حيث تشير الرموز إلى ما يأتي:
- V: حجم الغاز، ويقاس بوحدة اللتر.
- T: درجة حرارة الغاز، وتقاس بوحدة الكلفن.
- k: ثابت، وقيمته تعتمد على نوع الغاز، ووحدته لتر/كلفن.
قانون غاي - لوساك
ينص قانون غاي - لوساك (بالإنجليزية: Gay-Lussac’s Law)، على أنّ الضغط الذي يؤثره الغاز على الوعاء الموضوع فيه، يختلف باختلاف درجة الحرارة المطلقة لهذا الغاز، حيث تكون العلاقة بين الضغط الذي يؤثره الغاز ودرجة الحرارة علاقة طردية.
صاغ قانون غاي- لوساك الكيميائي الفرنسي جوزيف جاي لوساك في عام 1808 م، ويمكن تمثيل القانون بالصيغة الرياضية الآتية:
P / T = k
إذ تشير الرموز إلى ما يأتي:
- P: كمية الضغط الذي يؤثره الغاز في الوعاء الموضوع فيه، ويقاس بوحدة الباسكال.
- T: درجة الحرارة المطلقة للغاز، وتقاس بوحدة الكلفن.
- k: ثابت، وتختلف قيمته بحسب نوع الغاز ودرجة حرارته، ووحدته باسكال/كلفن.
قانون أفوجادرو
ينص قانون أفوجادرو (بالإنجليزية: Avogadro’s Law) على أنّ حجم أي غاز يتناسب مع عدد جزيئاته، حيث تُحسب عدد الجزيئات بالمول، إذ إنّه كلما زادت كمية الغاز يزداد حجمه، ويُذكر أنّ هذا القانون وُضع على يد الفيزيائي الإيطالي أماديو أفوجادرو في عام 1811 م، ويمكن تمثيل القانون بالصيغة الرياضية الآتية:
V=k×n
و في حال مقارنة غازين فإنّ العلاقة المستخدمة هي:
V1/n1=V2/n2
إذ تشير الرموز إلى ما يأتي:
- V: حجم الغاز، ويُقاس بوحدة اللتر.
- k: عدد جزيئات الغاز، وتُقاس بالمول.
- n: ثابت يعتمد على نوع الغاز، ويكون بوحدة (لتر.مول).
القانون العالم للغازات
يصف القانون العام للغازات المثالية (بالإنجليزية: General Ideal Gas Law) حركة جزيئات الغاز، بحيث تنتقل الجزيئات في مسارات عشوائية، وتتصادم مع بعضها البعض ومع جدران الوعاء الذي يحتوي الغاز، وتمارس هذه التصادمات ضغطًا على وحدة المساحة، وتتسبب أيضًا في احتلال الغازات للحجم.
يشغل الغاز مساحة صغيرة جدًا لأنّ الجسيمات الموجودة في الغاز ضئيلة للغاية، ويُذكر أنّ هناك عدد من العوامل التي يؤثر في حركة جزيئات الغاز، ومنها الضغط، والحجم، ودرجة الحرارة.
يجمع القانون العام للغازات بين كل من قانون بويل، وقانون شارل، وقانون جاي - لوساك، وقانون أفوجادرو في علاقة رياضية واحدة تصف العلاقة بين الضغط، والحجم، ودرجة الحرارة، وعدد مولات الغاز، ويمكن تمثيل القانون بالصيغة الرياضية الآتية:
(V = k × n × (T / P
إذ تشير الرموز إلى ما يأتي:
- P: هو كمية الضغط الذي يؤثره الغاز على الوعاء الموضوع فيه، ووحدتها باسكال
- T: درجة الحرارة، بوحدة الكلفن
- n: عدد المولات
- K: ثابت يعتمد على نوع الغاز ودرجة الحرارة، ووحدته ذرة. لتر/ مول. كلفن
- V: حجم الغاز، بوحدة اللتر
أمثلة على قوانين الغازات
فيما يأتي بعض الأمثلة على قوانين الغازات:
حساب الحجم النهائي للغاز
- ما الحجم النهائي (V2) لعينة من غاز حجمها الابتدائي (V1) يساوي 650 سم3 عند 25 س إذا سخنت إلى 400 س مع ثبات الضغط ؟
الحل:
- V1/ T1 = V2/ T2
- تعويض القيم مع تحويل درجة الحرارة من سيليسيوس إلى كلفن:
- 650 / (25 273) = V2/ (400 273)
- 650/ (298) = (V2 /(673
- V2 = 650 (673 / 298)
- V2 = 1,468 سم^3.
- تحويل الحجم إلى اللتر:
- V2 = 0.002 لتر
حساب عدد مولات الغاز
- احسب عدد مولات الهيدروجين الموجودة في 18 ل من الغاز عند ضغط قدره 70 cm.Hg، ودرجة حرارة 27 س علماً بأن (R = 0.0821 L. atm/K . mol)
الحل:
- P × v =n × R × T
- تعويض القيم مع تحويل الوحدات حسب النظام العالمي:
- ((0.0821) ×(27 273))/( n = ((70/67) ×18
- مول n = 0.673
حساب الحجم
- ما حجم الوعاء اللازم لاحتواء 0.0459 مول من غاز النيتروجين N2 في الظروف المعيارية علمًا أن قيمة الثابت k =22.4؟
الحل:
- V=k×n
- تعويض القيم مباشرة حيث V هو حجم وعاء الغاز اللازم لاحتواء 0.0459 مول من غاز النيتروجين في الظروف المعيارية.
- V = 0.0459 × 22.4
- لتر 1.3 =V
حساب حجم الغاز
- إذا كانت 4 لترات من غاز معين تحتوي على 0.960 مولًا من جزيئات الغاز، فإذا زادت كمية الغاز إلى 1.8 مولًا، فما هو الحجم الجديد الناتج من الغاز عند ثبوت الضغط ودرجة الحرارة.
الحل:
- V1/n1=V2/n2
- 4 /0.96 = V2/ 1.8
- V2 = (7.5 لتر)
حساب حجم الغاز
- عینة من غاز مثالي، فإذا كان حجمه (5 لتر)، تحت ضغط مقداره (15 atm)، فاحسب حجم هذا الغاز إذا علمت أن ضغطه أصبح (3 atm)، باعتبار درجة الحرارة ثابتة؟
الحل:
- p × V = c
- إدراج القانون الخاص بمقارنة غازين:
- p1 × V1 = p2 × V2
- (15 × 5 )= ( 3 × V2)
- V2 = (15 × 5 ) / 3
- V2 = 25 لتر
حساب عدد المولات
- احسب عدد مولات الهيدروجين الموجودة في 18 ل من الغاز عند ضغط مقداره 70 cm.Hg، ودرجة حرارة 27 سليزيوس، علماً بأن الثابت R له يساوي 0.0821
الحل:
- PV = n RT.
- n = PV/RT.
- تعويض القيم بعد تحويل الوحدات حسب النظام العالمي:
- ((27 273)×0.082)/(n= (70×18/7.
- n = 0.0673 مول.
ملاحظة: يجب الانتباه إلى تحويل درجة الحرارة من سلزيوس إلى كلفن.







