ارتفاع المثلث القائم
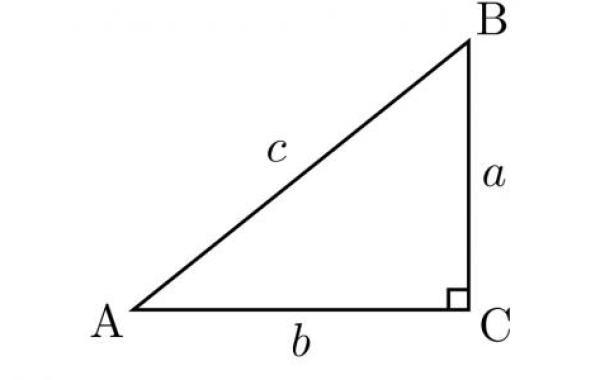
حساب ارتفاع المثلث القائم
يُمكن تعريف ارتفاع المثلث بأنّه طول العمود الساقط من إحدى زوايا المثلث وحتى الضلع المقابل لها، ويمتلك كل مثلث عادة ثلاثة ارتفاعات يرتبط كل منها بقاعدة مختلفة، أما بالنسبة للمثلث قائم الزاوية فيتم عادة اعتبار إحدى ساقيه على أنّها ارتفاعه، واعتبار الأخرى على أنّها القاعدة، حيث يتكون المثلث قائم الزاوية عادة من الوتر وهو الضلع الأطول والمقابل للزاوية القائمة، وساقين أو ضلعين آخرين يحصران بينهما الزاوية القائمة، إلا أنّه وفي بعض الأحيان يتم اعتبار الوتر هو القاعدة، وارتفاع المثلث هو العمود الواصل بين الزاوية القائمة للمثلث ووتره، وفي هذه الحالة يتم حساب الارتفاع باستخدام القانون الآتي:
ارتفاع المثلث قائم الزاوية = طول الساق الأولى للمثلث×طول الساق الثانية للمثلث/الوتر.
باستخدام المساحة
في بعض الأحيان تكون مساحة المثلث، وقاعدته معروفة، أمّا ارتفاعه فهو غير معروف، وبالتالي يمكن الحصول على ارتفاع المثلث من خلال إعادة ترتيب قانون مساحة المثلث، وذلك كما يأتي:
مساحة المثلث= 2/1×طول القاعدة×الارتفاع
وبالتالي فإن ارتفاع المثلث يساوي:
ارتفاع المثلث= (2×مساحة المثلث)/طول القاعدة
باستخدام نظرية فيثاغورس
يُمكن استخدام نظرية فيثاغورس عند معرفة طول الوتر والقاعدة لمعرفة ارتفاع المثلث القائم، في حال اعتبار إحدى الساقين هي الارتفاع، والتي تنص على أنّ:
مربع الوتر= مربع الضلع الأول (القاعدة) مربع الضلع الثاني (الارتفاع)
والمثال الآتي يوضّح ذلك:
مثال: مثلث قائم أب جـ طول قاعدته 12سم، والوتر فيه 24 سم، فما هو ارتفاعه؟
الحل:
- بالتعويض في نظرية فيثاغورس ينتج أن: 24² = 12² الارتفاع²، ومنه: 576 = 144 الارتفاع²، ومنه: الارتفاع²= 432، وباخذ الجذر التربيعي للطرفين ينتج أن: الارتفاع= 20.78سم.
باستخدام النسب المثلثية
يُمكن حساب ارتفاع المثلث القائم الزاوية أيضاً باستخدام النسب المثلثية، وهي جيب الزاوية، وجيب تمام الزاوية، وظلها، وذلك في حال معرفة قياس إحدى زواياه وطول القاعدة، أو طول الوتر، وذلك عند اعتبار إحدى الساقين هي الارتفاع؛ حيث إنّ:
- جيب الزاوية (جا)= الضلع المقابل للزاوية/الوتر.
- جيب تمام الزاوية (جتا)= الضلع المجاور للزاوية/الوتر.
- ظل الزاوية (ظا)= الضلع المقابل للزاوية/الضلع المجاور للزاوية.
أمثلة متنوعة على إيجاد ارتفاع المثلث القائم
حساب ارتفاع المثلث القائم باستخدام مساحته
المثال الأول: إذا كانت مساحة المثلث القائم 45م، وطول قاعدته 10م، فما هو ارتفاعه؟
الحل:
- بالتعويض في القانون: ارتفاع المثلث= (2×مساحة المثلث)/طول القاعدة = (2×45)/10= 9 م.
المثال الثاني: مثلث قائم طول قاعدته 8سم، ومساحته 24سم، فما هو ارتفاعه؟
الحل:
- بالتعويض في القانون: ارتفاع المثلث= (2×مساحة المثلث)/طول القاعدة = (2×24)/8= 6 سم.
المثال الثالث: مثلث قائم مساحته 10سم، وطول قاعدته 5سم، فما هو ارتفاعه؟
الحل:
- بالتعويض في القانون: ارتفاع المثلث= (2×مساحة المثلث)/طول القاعدة = (2×10)/5= 4 سم.
المثال الرابع: إذا كان ارتفاع مثلث قائم يزيد بمقدار 8سم عن ضعف طول قاعدته، وكانت مساحته 96سم²، جد قيمة ارتفاعه.
الحل:
- اعتبار طول القاعدة هو س، والارتفاع هو: 8 2س.
- بالتعويض في قانون: ارتفاع المثلث= (2×مساحة المثلث)/طول القاعدة، ينتج أن: 8 2س = (2×96)/س، وبضرب طرفي المعادلة في (س) ينتج أن: 8س 2س²= (96×2)، وبقسمة المعادلة على (2) ينتج أن: س² 4س-96=0.
- بحل المعادلة التربيعية ينتج أن: س= 8سم، وهي قيمة طول القاعدة، أما الارتفاع فهو: 8 2س = 8 2×8 = 24سم.
حساب ارتفاع المثلث باستخدام النسب المثلثية
المثال الخامس: وقف أحمد على بعد 30 دسم من قاعدة إحدى الأشجار، وكانت الزاوية المحصورة بين الخط الممتد من قدميه نحو قمة الشجرة، والخط الواصل بين قدميه وقاعدة الشجرة هو 57 درجة، جد ارتفاع هذه الشجرة.
الحل:
- تصنع الشجرة مثلثاً قائم الزاوية مع أحمد وتره هو الخط الممتد من قدمي أحمد نحو قمة الشجرة، وارتفاعه هو ارتفاع الشجرة، أما طول قاعدته فهو طول الخط الممتد من قدمي أحمد نحو قاعدة الشجرة، وعليه يُمكن حساب ارتفاع المثلث باستخدام قانون ظل الزاوية وهو: ظا الزاوية= الضلع المقابل للزاوية/الضلع المجاور للزاوية، وعليه:
- ظا (57) = ارتفاع الشجرة/الخط الواصل بين قدمي أحمد وقاعدة الشجرة = ارتفاع الشجرة/30، ومنه: ارتفاع الشجرة= 46.20 دسم.
المثال السادس: إذا تم استخدام سلم بطول 6م للوصول إلى إحدى النوافذ في أحد المباني، وكانت الزاوية المحصورة بين السلم والأرض 60 درجة، جد ارتفاع النافذة عن سطح الأرض.
الحل:
- تصنع النافذة مع السلم مثلثاً قائم الزاوية وتره هو السلم، أما الخط الممتد من قاعدة السلم نحو النافذة فهو القاعدة، وارتفاعه هو ارتفاع النافذة عن سطح الأرض، وعليه يُمكن حساب ارتفاع النافذة عن سطح الأرض باستخدام قانون جيب الزاوية وهو: جا الزاوية= الضلع المقابل للزاوية/الوتر، وعليه:
- جا (60) = ارتفاع النافذة عن سطح الأرض/طول السلم = ارتفاع النافذة عن سطح الأرض/6، ومنه: ارتفاع النافذة عن سطح الأرض= 5.2م.
حساب ارتفاع المثلث باستخدام نظرية فيثاغوروس
المثال السابع: إذا كان طول الوتر في المثلث قائم الزاوية هو 5سم، وطول إحدى الساقين 3سم، جد ارتفاع المثلث الواصل بين الزاوية القائمة، والوتر.
الحل:
- بالتعويض في القانون: ارتفاع المثلث= طول الساق الأولى للمثلث×طول الساق الثانية للمثلث/الوتر ينتج أن: ارتفاع المثلث= 3×طول الساق الثانية للمثلث/5.
- لحساب طول الساق الثانية يجب التعويض في قانون فيثاغورس لينتج أن: مربع الوتر= مربع الضلع الأول مربع الضلع الثاني ، 5²= 3² مربع الضلع الثاني، ومنه: الضلع الثاني= 4سم.
- تعويض القيمة السابقة في القانون: ارتفاع المثلث= 3×4/5 = 3.75 سم.
المثال الثامن: إذا كان ارتفاع مثلث قائم يقل بمقدار 7سم عن طول قاعدته، وكان طول وتره 13سم، جد قيمة ارتفاعه.
الحل:
- اعتبار الارتفاع هو س، وطول القاعدة هو س 7.
- بالتعويض في القانون: مربع الوتر= مربع الضلع الأول مربع الضلع الثاني ينتج أن: 13² = س² (س 7)²، ومنه: 169 = س² (س² 14س 49)، 2س² 14س-120=0.
- بحل المعادلة التربيعية ينتج أن: س= 5سم، وهي قيمة الارتفاع.
يُعتبر ارتفاع المثلث قائم الزاوية هو أحد ضلعيه اللذين يحصران الزاوية القائمة أو هو العمود النازل من رأس الزاوية القائمة على الوتر، ويُمكن حساب ارتفاع المثلث القائم الزاوية بمعرفة مساحته وأحد ضلعيه، أو بمعرفة إحدى الزوايا وتطبيق قوانين النسب المثلثية، أو باستخدام نظرية فيثاغوروس.







