مفهوم البوابات المنطقية
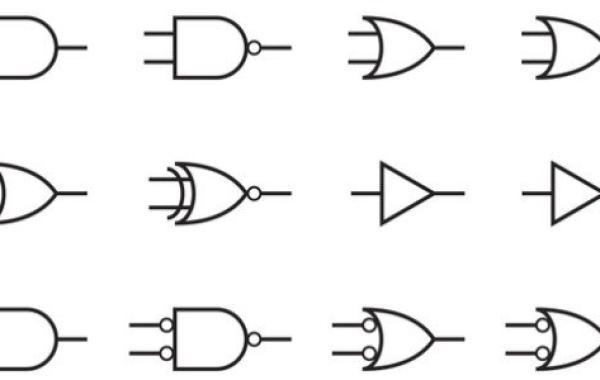
البوابات المنطقية الأساسية
تُعدّ البوابات المنطقية عنصراً أساسياً في أي نظام رقمي، حيث تكون على شكل دارة إلكترونية بسيطة تتواجد في الحواسيب ممثّلةً بالنظام الثنائي (بالإنجليزية: Binary Number) المبني على 1 و0، وتُقسم البوابات المنطقية إلى نوعين رئيسيين؛ البوابات المنطقية الأساسية والبوابات المنطقية المُشتقة، وفيما يأتي أنواع البوابات المنطقية الأساسية:
بوابة AND
تُسمّى (وَ)، وتضمّ مدخلَين ومخرجاً واحداً، وتُعامل معاملة عملية الضرب في الرياضيات، كما هو موضح أدناه:
- 1 (AND) 0 تُعطي 0.
- 0 (AND) 1 تُعطي 0.
- 0 (AND) 0 تُعطي 0.
- 1 (AND) 1 تُعطي 1.
لو فرضنا أنّ المدخلَين المتغيرين لبوابة (AND) اسمهما (X) و (A)، بينما المخرج هو المتغيّر (B)، يُمكن إنشاء جدول خاص اسمه (جدول الحقيقة لِبوابة (AND))، كما يأتي:
| A | X | B = X (AND) A |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
لذا وممّا سبق فإنّ مخرجات بوابة (AND) المنطقية الأساسية هي كالآتي:
- تُعطي مخرج قيمته 1 عندما تكون قيمة المدخلَين 1 فقط.
- تُعطي مخرج قيمته 0 عندما تكون قيمة أحد المدخلَين أو كلاهما 0.
بوابة OR
تُسمّى (أو)، وتضمّ مدخلَين ومخرج واحد، وتُعامل معاملة عملية الجمع في الرياضيات، كما هو موضح أدناه:
- 0 (OR) 1 تُعطي 1.
- 1 (OR) 0 تُعطي 1.
- 0 (OR) 0 تُعطي 0.
- 1 (OR) 1 تُعطي 1 وليس 2، حيث تُعدّ هذه الحالة الوحيدة التي لا تنطبق عليها عملية الجمع في بوابة OR.
لو فرضنا أنّ المدخلَين المتغيرين لبوابة (OR) اسمهما (B) و (A)، بينما المخرج هو المتغيّر (X)، يُمكن إنشاء جدول خاص اسمه (جدول الحقيقة لبوابة (OR))، كما يأتي:
| A | B | X = B (OR) A |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
لذا وممّا سبق فإنّ مخرجات بوابة (OR) المنطقية الأساسية هي كالآتي:
- تُعطي مخرج قيمته 0 عندما تكون قيمة المدخلَين 0 فقط.
- تُعطي مخرج قيمته 1 عندما تكون قيمة أحد المدخلَين أو كلاهما 1.
بوابة NOT
تُسمّى العاكِس، وبوابة النفي المنطقية، وتضمّ مدخلاً واحداً ومخرجاً واحداً، وسُمّيت العاكِس لأنّها تُعطي نتيجة مُعاكسة كما هو موضح أدناه:
- NOT) 0) تُعطي 1.
- NOT) 1) تُعطي 0.
لو فرضنا أنّ المدخل المتغيّر لبوابة (NOT) اسمه (X) والمخرج هو المتغيّر (A)، يُمكن إنشاء جدول خاص اسمه (جدول الحقيقة لِبوابة (NOT))، كما يأتي:
| X | A = (NOT) X |
| 1 | 0 |
| 0 | 1 |
لذا ومما سبق فإنّ مخرجات بوابة (NOT) المنطقية الأساسية هي كالآتي:
- تُعطي مخرج قيمته 0 عندما تكون قيمة المدخل 1 فقط.
- تُعطي مخرج قيمته1 عندما تكون قيمة المدخل 0 فقط.
بوابة XOR
اشتُقّ اسمها من دمج كلمة (eXclusive) و(OR)، وتضمّ مدخلَين ومخرجاً واحداً كما هو موضح أدناه:
- 1 (XOR) 0 تُعطي 1.
- 0 (XOR) 1 تُعطي 1.
- 0 (XOR) 0 تُعطي 0.
- 1 (XOR) 1 تُعطي 0.
لو فرضنا أنّ المدخلّين المتغيرين لبوابة (XOR) اسمهما (B) و (A)، بينما المخرج هو المتغيّر (X)، يُمكن إنشاء جدول خاص اسمه (جدول الحقيقة لِبوابة (XOR))، كما يأتي:
| A | B | X = B (XOR) A |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
لذا ومما سبق فإنّ مخرجات بوابة (XOR) المنطقية الأساسية هي كالآتي:
- تُعطي مخرجاً قيمته 0 عندما تكون قيمة المدخلين متساويتين (0,0) أو (1,1).
- تُعطي مخرجاً قيمته1 عندما تكون قيمة المدخلين مختلفين (0,1) أو (1,0).
البوابات المنطقية المشتقة
هي البوابات المنطقية التي اشتُقّت من البوابات المنطقية الأساسية، وهي كالآتي:
بوابة NAND
سمّيت بهذا الاسم لأنها ناتجة من دمج البوابتين الأساسيتين (AND) و(NOT) لذا فهي عكس بوابة (AND)، كما أنّها إختصار لـ AND NOT أي نفي ال AND، وتضمّ مدخلَين ومخرجاً واحداً، وتُعامل معاملة عملية الضرب في الرياضيات، ثمّ تُعكس النتيجة، كما هو موضح أدناه:
- 1 (NAND) 0 تُعطي 1.
- 0 (NAND) 1 تُعطي 1.
- 0 (NAND) 0 تُعطي 1.
- 1(NAND) 1 تُعطي 0.
لو فرضنا أنّ المدخلَين المتغيرين لبوابة (NAND) اسمهما (X) و (B)، بينما المخرج هو المتغيّر (Y)، يُمكن إنشاء جدول خاص اسمه (جدول الحقيقة لِبوابة (NAND))، كما يأتي:
| X | B | Y = B (NAND) X |
| 1 | 0 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 0 | 0 | 1 |
لذا ومما سبق فإنّ مخرجات بوابة (NAND) المنطقية المشتقة هي كالآتي:
- تُعطي مخرجاً قيمته 0 عندما تكون قيمة كلا المدخلين1 فقط.
- تُعطي مخرجاً قيمته 1 عندما تكون قيمة أحد المدخلَين أو كلاهما 0.
بوابة NOR
سمّيت NOR بهذا الاسم لأنها اشتُقّت من دمج البوابتين الأساسيتين (NOT) و(OR) لذا فهي عكس بوابة (OR)، أيّ أنّها إختصار لـ OR NOT أي نفي ال OR، وتضمّ مدخلَين ومخرجاً واحداً، وتُعامل معاملة عملية الجمع في الرياضيات، ثمّ تُعكس النتيجة، كما هو موضح أدناه:
- 0 (NOR) 1 تُعطي 0.
- 1 (NOR) 0 تُعطي 0.
- 0 (NOR) 0 تُعطي 1.
- 1 (NOR) 1 تُعطي 0.
لو فرضنا أنّ المدخلَين المتغيرين لبوابة (NOR) اسمهما (A) و (B)، بينما المخرج هو المتغيّر (X)، يُمكن إنشاء جدول خاص اسمه (جدول الحقيقة لِبوابة (NOR))، كما يأتي:
| A | B | X = B (NOR) A |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
لذا ومما سبق فإنّ مخرجات بوابة (NOR) المنطقية المشتقة هي كالآتي:
- تُعطي مخرج قيمته 1 عندما تكون قيمة كلا المدخلَين 0 فقط.
- تُعطي مخرج قيمته 0 عندما تكون قيمة أحد المدخلَين أو كلاهما 1.
بوابة Buffer
كلمة (Buffer) تعني العازل، وسمّيت بهذا الاسم لأنّها البوابة المنطقية الأساسية التي تُمرر مدخلاتها إلى المخرجات دون تغيير، وقد اشتُقّت من دمج البوابتين الأساسيتين (NOT) و(NOT) لذا فهي عكس بوابة (NOT)، بمعنى أنّها تُمثّل عكس النفي، وتضمّ مدخلاً واحداً ومخرجاً واحداً، لذا فهي تُمثّل أبسط أشكال البوابات المنطقية بنوعيها الأساسية والمشتقة، كما هو موضح أدناه:
- 0 (Buffer) 0 تُعطي 0.
- 1 (Buffer) 1 تُعطي 1.
لو فرضنا أنّ المدخلَين المتغيرين لبوابة (Buffer) اسمهما (B) و(A)، بينما المخرج هو المتغير (X)، يُمكن إنشاء جدول خاص اسمه (جدول الحقيقة لِبوابة (Buffer))، كما يأتي:
| A | B | X |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
لذا وممّا سبق فإنّ مخرجات بوابة (Buffer) المنطقية المشتقة هي كالآتي:
- تُعطي مخرج قيمته 0 عندما يكون المدخلَين متساويين وقيمة كلّ منهما 0.
- تُعطي مخرج قيمته 1 عندما يكون المدخلين متساويتين وقيمة كلّ منهما 1.
بوابة XNOR
تُسمّى بوابة اختيار حصري سالبة، وسمّيت بهذا الاسم لاشتقاقه من دمج كلمة (eXclusive) و(NOR)، لذا فهي عكس بوابة (XOR )، وتضمّ مدخلَين ومخرجاً واحداً، كما هو موضح أدناه:
- 0 (XNOR) 0 تُعطي 1.
- 0 (XNOR) 1 تُعطي 0.
- 1 (XNOR) 0 تُعطي 0.
- 1 (XNOR) 1 تُعطي 1.
لو فرضنا أنّ المدخلَين المتغيّرين لبوابة (XNOR) اسمهما (B) و(A)، بينما المخرج هو المتغيّر (X)، يُمكن إنشاء جدول خاص اسمه (جدول الحقيقة لِبوابة (XNOR))، كما يأتي:
| A | B | X=A(XNOR)B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
لذا ومما سبق فإن مخرجات بوابة (XNOR) المنطقية المشتقة هي كالآتي:
- تُعطي مخرج قيمته 1 عندما تكون قيمة المدخلَين متساويتين (0,0) أو (1,1).
- تُعطي مخرج قيمته 0 عندما تكون قيمة المدخلَين مختلفين (0,1) أو (1,0).
أنواع البوابات المنطقية الرئيسية هي البوابات الأساسية والمُشتقة، والبوابات الأساسية هي: AND ،OR ،NOT ،XOR، في حين أنّ البوابات المشتقة هي: NAND ،NOR ،Buffer ،XNOR، ولكلّ منها مداخل ومخارج، ويجري التعامل معها كمعادلات رياضية.
استخدامات البوابات المنطقية
فوائد البوابات المنطقية لا تعدّ ولا تُحصى، فهي تدخل في العديد من الصناعات التكنولوجية، ومن أبرزها ما يأتي:
- بناء م عالجات الأجهزة الإلكترونية.
- برمجة الحواسيب.
- صناعة مضخات خزانات المياه.
- صناعة الأجهزة والمعدات الطبية.
- صناعة أشباه الموصلات ( بالإنجليزية: Transistor).
- صناعة الساعات الرقمية والمؤقتات الزمنية.
أولويات البوابات المنطقية
هناك أولويات خاصّة يجب اتّباعها عند إيجاد ناتج البوابات المنطقية للجمل التي تحتوي على أكثر من بوابة منطقية، وفيما يأي ترتيب الأولويات بدءًا من الأعلى إلى الأقل:
- الأقواس.
- NOT.
- AND.
- OR.
- في حال تساوت الأولويات، يجب البدء من يسار المعادلة إلى يمينها.
أمثلة على أولويات البوابات المنطقية
هناك الكثير من الأمثلة على عبارات أولويات البوابات المنطقية، ولإيجاد الناتج يجب مراعاة الأولويات للحصول على النتيجة الصحيحة.
1OR 0 AND 1
- تحديد الأولوية، الأولوية تكون لبوابة AND بما أنّ العبارة تخلو من الأقواس.
- إيجاد ناتج العبارة 0AND 1
- 0
- إيجاد ناتج العبارة 1OR 0
- الناتج = 1.
NOT 0 AND (NOT 1 OR 0)
- إيجاد ناتج داخل الأقواس، شريطة إعطاء الأولوية لبوابة NOT ثمّ OR.
- إيجاد ناتج خارج الأقواس، شريطة إعطاء الأولوية لبوابة NOT ثمّ AND.
- NOT 0 AND (0 OR 0)
- NOT 0 AND 0
- 1AND 0
- الناتج = 0.
A AND B OR NOT C
علماً بأنّ: A=0 , B=1, C=1
- تعويض المعطيات: 0AND 1 OR NOT 1
- تحديد الأولوية، تُعطى الأولوية لبوابة NOT، فبوابة AND، ثمّ بوابة OR.
- 0AND 1 OR 1
- 0OR 0
- الناتج = 0.
A OR NOT B) AND (NOT C AND D))
علماً بأنّ: A=0 , B=1, C=1, D=0
- تعويض المعطيات:
- 0OR NOT 1) AND (NOT 1 AND 0 ))
- تحديد الأولوية، بسبب تساوي الأولويات، يتمّ حل القوس الأيسر ثمّ القوس الأيمن:
- 0OR 0) AND (NOT 1 AND 0))
- 0ِAND (NOT 1 AND 0)
- 0ِAND (0 AND 0)
- 0AND 0
- الناتج = 0.
تُعدّ البوابات المنطقية بنوعيها الأساسي أو المشتق مهمّةً في كافّة أشكال الصناعات التقنية الحديثة، لذا يُولى إليها اهتمام كبير، ويُذكر أنّه لحلّ البوابات المنطقية المعقدة يجب اتّباع بعض الأولويات التي تُسهّل التعامل معها.







