معادلة برنولي
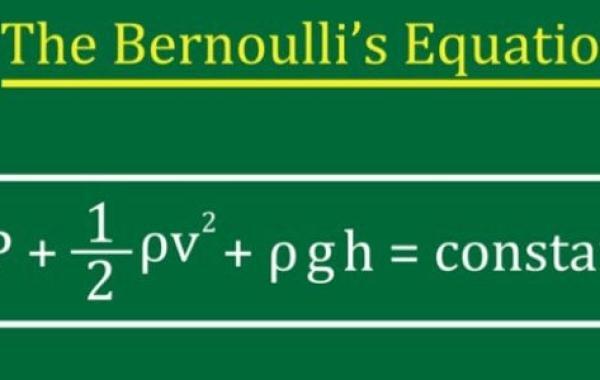
الصيغة الرياضية لمعادلة برنولي
تربط معادلة برنولي بين الضغط والسرعة والارتفاع لأي نقطتين في سائل انسيابي التدفق ذي كثافة ثابتة، وهي معادلة شاملة لمبدأ برنولي الذي يأخذ بعين الاعتبار التغيرات في طاقة الجاذبية الكامنة، وتعتمد معادلة برنولي على مبدأ حفظ الطاقة لتدفق السائل بحيث الطاقة الإجمالية للسائل قبل تحركه تساوي الطاقة الإجمالية للسائل بعد تحركه، ويُمكن تمثيلها بالصيغة الرياضية التالية:
ضغط السائل عند النقطة الأولى 1/2 × كثافة السائل × مربع سرعة السائل عند النقطة الأولى كثافة السائل × تسارع الجاذبية الأرضية × ارتفاع السائل عند النقطة الأولى= ضغط السائل عند النقطة الثانية 1/2 × كثافة السائل × مربع سرعة السائل عند الثانية كثافة السائل × تسارع الجاذبية الأرضية × ارتفاع السائل عند النقطة الثانية
وبالرموز:
ض1 1/2 ث ع1 ث جـ أ1 = ض2 1/2 ث ع2 ث جـ أ2
ويُمكن تمثيله بالرموز الإنجليزية:
p1 1/2 ρ v1² ρgh1 = p2 1/2 ρ v2² ρgh2
حيث أنّ:
- p أو ض: ضغط السائل، ويُقاس بوحدة نيوتن لكل متر مربع (نيوتن/م²).
- v أو ع: سرعة السائل، ويُقاس بوحدة متر لكل ثانية (م/ث).
- ρ أو ث: كثافة السائل، وتُقاس بوحدة كيلوغرام لكل متر مكعب (كغ/م³).
- h أو أ: ارتفاع السائل ويُقاس بوحدة المتر (م).
- g أو جـ: ثابت الجاذبية الأرضية ويساوي 9.8 م/ث².
الصيغة الرياضية لمعادلة برنولي في السوائل الساكنة
عندما يكون السائل ساكنًا فإنّ سرعته تبقى ثابتة وتساوي صفر، ولذلك فإنّ سرعة السائل الابتدائية تساوي سرعته النهاية وتساوي صفر (v1 = v2 = 0)، فتُصبح معادلة برنولي كما يلي:
ضغط السائل عند النقطة الأولى كثافة السائل × تسارع الجاذبية الأرضية × ارتفاع السائل عند النقطة الأولى= ضغط السائل عند النقطة الثانية كثافة السائل × تسارع الجاذبية الأرضية × ارتفاع السائل عند النقطة الثانية
وبالرموز:
ض1 ث جـ أ1 = ض2 ث جـ أ2
ويُمكن تمثيله بالرموز الإنجليزية:
p1 ρgh1 = p2 ρgh2
حيث أنّ:
- p أو ض: ضغط السائل ويُقاس بوحدة نيوتن لكل متر مربع (نيوتن/م²).
- ρ أو ث: كثافة السائل وتُقاس بوحدة كيلوغرام لكل متر مكعب (كغ/م³).
- h أو أ: ارتفاع السائل ويُقاس بوحدة المتر (م).
- g أو جـ: ثابت الجاذبية الأرضية ويساوي 9.8 م/ث².
الصيغة الرياضية لمعادلة برنولي في العمق الثابت
وهناك حالات أيضًا يتدفق فيها السائل بعمق ثابت، وهي تنطبق على السوائل ذات الأحجام الصغيرة التي تتدفق على طول مسار أفقي، بحيث يكون ارتفاع السائل الابتدائي يساوي ارتفاعه النهائي ويساوي صفر (h1 = h2 = 0)، فتُصبح معادلة برنولي كما يلي:
ضغط السائل عند النقطة الأولى 1/2 × كثافة السائل × مربع سرعة السائل عند النقطة الأولى = ضغط السائل عند النقطة الثانية 1/2 × كثافة السائل × مربع سرعة السائل عند الثانية.
وبالرموز:
ض1 1/2 ث ع1 = ض2 1/2 ث ع2
ويُمكن تمثيله بالرموز الإنجليزية:
p1 1/2 ρ v1² = p2 1/2 ρ v2²
حيث أنّ:
- p أو ض: ضغط السائل ويُقاس بوحدة نيوتن لكل متر مربع (نيوتن/م²).
- v أو ع: سرعة السائل ويُقاس بوحدة متر لكل ثانية (م/ث).
- ρ أو ث: كثافة السائل وتُقاس بوحدة كيلوغرام لكل متر مكعب (كغ/م³).
أمثلة حسابية على معادلة برنولي
وفيما يأتي بعض الأمثلة الحسابية على معادلة برنولي:
حساب ضغط السائل
إذا تدفق الماء ذو الكثافة 10 كغ/م³ في خرطوم من ارتفاع 7م إلى ارتفاع 3م، بحيث زادت سرعته من 2 م/ث إلى 15م/ث وكان ضغطه عند هذه السرعة يساوي 1.5×10 نيوتن/م²، جد ضغط الماء الابتدائي.
الحل:
- نكتب المعطيات:
- ث = 1×10 كغ/م³
- ع1 = 2 م/ث
- أ1 = 7 م/ث
- أ2 = 3 م/ث
- ع2 = 15 م/ث
- ض2 = 1.5×10 نيوتن/م²
- نعوض المعطيات في القانون: ض1 1/2 ث ع1 ث جـ أ1 = ض2 1/2 ث ع2 ث جـ أ2
- ض1 1/2 × 10 × 2² 10 × 9.8 × 7 = 1.5 × 10 1/2 × 10 × 15² 10 × 9.8 × 3
- ض1 = 2.2×10 نيوتن/م²
حساب ضغط السائل الساكن
يتدفق سائل ساكن كثافته تساوي 1090 كغ/م³ من ارتفاع 1.2م إلى الأرض، بحيث كان ضغطه عند ارتفاع 1.2 م يساوي 4080 نيوتن/م² جد ضغط السائل عند وصوله إلى الأرض.
الحل:
- نُلاحظ أنّ السائل ساكن إذًا: ع1 = ع2 = 0
- وبالتالي نستخدم القانون التالي لإيجاد ضغط السائل على الأرض: ض1 ث جـ أ1 = ض2 ث جـ أ2
- نكتب المعطيات:
- ض1 = 4080 نيوتن/م²
- أ1 = 1.2 م/ث
- أ2 = 0 م/ث
- ث = 1090 كغ/م³
- نعوض المعطيات في القانون:
- 4080 1090 × 9.8 × 1.2 = ض2 0
- (ض2) = ضغط السائل على الأرض = 16.9 كيلو نيوتن/م²
حساب ضغط السائل في العمق ثابث
يتدفق سائل ذو كثافة ثابتة تساوي 960 كغ/م³ بثبات عبر أنبوب، إذا علمتَ أنّ ضغط السائل عند نقطة البداية يساوي 200 كيلو نيوتن/م² وسرعته 5 م/ث، بينما تصبح سرعته عند نقطة النهاية 7.8 م/ث، احسب مقدار ضغط السائل عند نقطة النهاية.
الحل:
- نُلاحظ أنّ العمق ثابت إذًا: أ1 = أ2 = 0
- وبالتالي نستخدم القانون التالي لإيجاد الضغط عند نقطة النهاية: ض1 1/2 ث ع1 = ض2 1/2 ث ع2
- نكتب المعطيات:
- ض1= 200 × 10^3 نيوتن/م²
- ث = 960 كغ/م³
- ع1 = 5 م/ث
- ع2 = 7.8 م/ث
- نعوض المعطيات في القانون: ض1 1/2 ث ع1 = ض2 1/2 ث ع2
- نُعيد ترتيب القانون: ض2= ض1 1/2 ث ع1 - 1/2 ث ع2
- 1/2 × 960 × 7.8^2 - 1/2 × 960 × 5^2 3^10×200 = ض2
- (ض2) = ضغط السائل عند نقطة النهاية = 182.8 كيلو نيوتن/م²
تطبيقات عملية على معادلة برنولي
فيما يلي أبرز التطبيقات على معادلة برنولي:
- الشرب باستخدام المصاصة أو القشة: عندما تُستخدم القشة للشرب تُصبح إحدى تطبيقات معادلة برنولي، وذلك عند استخدامها يتحرك الهواء داخلها بشكل أسرع فيكون الهواء الموجود عند الحافة العلوية للمصاصة أسرع وضغطه أقل، بينما يكون الهواء عند الحافة السفلية القريبة من المشروب سرعته أقل وضغطه أكبر، ونتيجة هذا الاختلاف في الضغط فإنّ السائل ينتقل من الضغط المرتفع إلى الضغط المنخفض فيرتقع ويصل إلى الفم.
- المدخنة: ترتفع درجة حرارة الهواء في المدخنة نتيجة الاحتراق، وعند ارتفاع درجة حرارة الهواء تقل كثافته فيرتفع للأعلى ويُصبح تدفقه أسرع، ووفقًا لمعادلة برنولي فإنّه عندما يكون معدل تدفق الهواء مرتفعًا فإنّ ضغطه يكون أقل ولذلك يرتفع الدخان من داخل المدخنة إلى خارجها أي من الضغط المرتفع إلى الضغط المنخفض.
- جحر الفئران في الأرض: نظرًا لحاجة الفئران داخل الأرض للتنفس، فإنّها تقوم بحفر ثقبين على ارتفاعات مختلفة داخل الأرض ليتمكن الهواء من المرور عبرها، وعندما يتدفق الهواء خلال ارتفاعات مختلفة فإنّ سرعة تدفقه تزداد وبالتالي ضغطه يقل، فينتقل الهواء من الضغط المرتفع إلى الضغط المنخفض عبر الجحر.
- أجنحة الطائرة والرفع الديناميكي: صُمم جناح الطائرة ليكون منحنيًا ليُساعد الطائرة على الطيران، بحيث يكون الجزء الأمامي منه سمكيًا مقارنةً بالجزء الخلفي، وعند تحريك الطائرة للأمام فإنّ الهواء يتدفق من أسفل الجناح إلى أعلاه، وبالتالي تزداد سرعة الهواء في أعلى الجناح فيقل ضغطه، ونظرًا لاختلاف فرق الضغط بين أعلى وأسفل الجناح يؤدي ذلك إلى رفع الطائرة للأعلى.
تُطبق معادلة برنولي قانون حفظ الطاقة وتربط بين الضغط والارتفاع وسرعة السائل، بحيث يساوي الضغط والطاقة الحركية وطاقة الوضع للسائل قبل تدفقه الضغط والطاقة الحركية وطاقة الوضع الجاذبية بعد تدفقه أو تحركه، وعندما يُطبق القانون للسوائل الساكنة فإنّ سرعة السائل تساوي صفر وبالتالي الطاقة الحركية للسائل تساوي صفر، وعندما يُطبق القانون على عمق ثابت فإنّ طاقة وضع الجاذبية للسائل تساوي صفر.







