قوانين اشتقاق الدوال
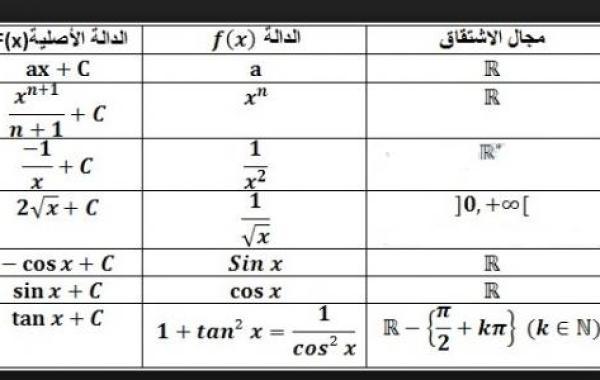
الدوال
تُعرّف الدالة المشتقة بأنّها ميل المماس لمنحنى ق (س) عند أي نقطة بشرط وجود هذه المشتقة، كما أنّنا لا نستطيع القول إنّ المشتقة موجودة إلا إذا كانت النهاية موجودة من اليمين واليسار عند نقطة معينة.
إنّ معدل تغير الاقتران أو المشتقة الأولى للاقتران ق (س) عند س=س1 وفي مجاله يُرمز له بالرمز ق(س1)، كما يُستخدم الرمز ق(س1) للتعبير عن المشتقة الثانية للاقتران ق (س)، وبصورة عامة فإنّ رمز المشتقة ن للاقتران ق (س) عند س=س1 هي ق (س) حيث إنّ ن=1، 2، 3، 4، 5.
استُخدم تعريف المشتقة لوقت طويل حتى يتم إيجادها، وبعد جهود ودراسات عديدة تم تسهيل الحصول على المشتقة من خلال تدوين مجموعة من القواعد سُميت بقواعد اشتقاق الدوال التي سنعرفكم على بعضها في هذا المقال.
قوانين اشتقاق الدوال
قاعدة العدد الثابت
إذا كان ق (س)=جـ، حيث جـ عدد ثابت، فإنّ ق (س)=0 فكلّ س تنمي إلى مجموعة الأعداد الحقيقة.
مثال:
| إذا كان ق (س)=2.5، أوجد ق (4)، ق (س) |
|---|
| ق (س)=0 لجميع قيم س التي تنتمي إلى مجموعة الأعداد الحقيقية ق (4)=0 لأنّ 4 تنتمي إلى مجموعة الأعداد الحقيقية |
قاعدة الاقتران كثير الحدود
إذا كان ق (س)=س، حيث إنّ ن تنتمي مجموعة الأعداد الطبيعية بدون العدد صفر، فإنّ ق (س)=ن س.
مثال:
| إذا كان ق (س)=س، فأوجد ق (س)، ق (-2) |
|---|
| ق (س)=6 س ق (-2)=6 (-2) ق (-2)=-192 |
قاعدة الجمع والطرح
إذا كان ق (س)، هـ (س) اقتراناً قابلاً للاشتقاق عند س، وكانت جـ تنتمي مجموعة الأعداد الحقيقية فإنّ:
- ك (س)=جـ×ق (س) قابل للاشتقاق عند س، ويكون ك (س)=جـ×ق (س).
- ع (س)=ق (س) هـ (س) قابل للاشتقاق عند س، ويكون ع (س)=ق (س) هـ (س).
- ل (س)=ق (س)-هـ (س) قابل للاشتقاق عند س، ويكون ل (س)=ق (س)-هـ (س).
مثال 1:
| إذا كان ق (س)=5 س 4 س 2 س، أوجد ق (س) |
|---|
| ق (س)=25 س 16 س 4 س |
مثال 2:
| إذا كان ق (س)=2 س، ع (س)=5 س، ل (س)=ق (س)-ع (س)، أوجد ل (س) |
|---|
ق (س)=2 ع (س)=5 ل (س)=2-5 ل (س)=-3 |
قاعدة الضرب
مشتقة حاصل ضرب اقترانين: إذا كان كلّ من ق (س)، هـ (س) اقترانين قابلين للاشتقاق عند س، وكان ع (س)=ق (س)×هـ (س) فإنّ: الاقتران ع (س) قابل للاشتقاق عند س، ويكون ع (س)=ق (س)×هـ (س) ق (س)×هـ (س).
مثال:
| أوجد مشتقة الاقتران ك (س)=(س 1) (س 2) |
|---|
بتطبيق قانون ضرب اقترانين فإنّ: ك (س)=(س 1) (1) (س 2) (4س) ك (س)=4س 8 س س 1 ك (س)=5س 8 س 1 |
قاعدة القسمة
مشتقة ناتج قسمة اقترانين: إذا كان كل من ق (س)، ع (س) قابلاً للاشتقاق عند س، ع (س) لا يساوي صفر، فإنّ: غ (س)=ق (س)/ع (س) قابل للاشتقاق عند س، ويكون غ (س)=[ق (س)×ع (س)]-[ع (س)×ق (س)]/(ع (س)).
مثال :
| إذا كان ق (س)=(3 س 1)/ (2 س-5) بحيث إنّ س لا تساوي 5/2، فأوجد ق (س) |
|---|
بتطبيق قانون مشتقة قسمة اقترانين فإنّ: ق (س)=(2س-5)×3 -(3س 1)×2/(2 س-5) ق (س)=-17/(2 س-5)، س لا تساوي 5/ 2 |
قاعدة السلسلة
مشتقة الاقتران المركب: إذا كان الاقتران هـ (س) قابلاً للاشتقاق عند النقطة س، وكان ق (س) قابلاً للاشتقاق عند هـ (س)، فإنّ الاقتران المركب (قοهـ) (س) يكون قابلاً للاشتقاق عند س، ويكون (قοهـ) (س)=ق (هـ (س))×هـ (س).
مثال :
| إذا كان ق (س)=س 5، هـ (س)=س 1 فأوجد: (قοهـ) (س) |
|---|
| ق (س)=2س، هـ (س)=2س (قοهـ) (س)=ق (هـ (س))×هـ (س) (قοهـ) (س)=ق(س 2س) (قοهـ) (س)=2 (س 1)×2س (قοهـ) (س)=4 (س س) (قοهـ) (س)=4س 4 س |
قاعدة القوى الكسرية
مشتقة القوى الكسرية: إذا كانت ص=س ، حيث إنّ (م/ن) عدد نسبي فإن دص/دس=(م/ن) س.
مثال :
| إذا كان ق (س)=س، فأوجد ق(8) |
|---|
| ق (س)=(2/3) س ق(8)=(2/3)8 ق(8)=(2/ 3)×(2) ق(8)=(2 /3)×2 ق(8)=(2/ 3)×(1/ 2) ق(8)=1 /3 |
قواعد الاقترانات الدائرية
- النظرية 1: إذا كان ق (س)=جاس، فإنّ ق (س)=جتاس.
- النظرية 2: إذا كان ق (س)=جتاس، فإن ق (س)=-جاس.
- النظرية 3: إذا كان ص=ظاس، فإنّ دص / دس=قاس.
- النظرية 4: إذا كان ص=ظتاس، فإنّ دص / دس=-قتاس.
- النظرية 5: إذا كان ص=قاس، فإنّ دص / دس=قاس ظاس.
- النظرية 6: إذا كان ص=قتاس، فإنّ دص / دس=-قتاس ظتاس.
مثال 1:
| إذا كان ق (س)=جاس، فأوجد ق(Π/6) |
|---|
ق (س)=جتاس ق (س)=جتا(Π / 6) ق (س)=3 /2 |
مثال 2:
| إذا كان هـ (س)=س جاس، فأوجد هـ (س) |
|---|
هـ (س)=س×جتاس جاس×1 هـ (س)=س جتاس جاس |
مثال 3:
| إذا كان جتا(س ص)=س، فأوجد دس/دص |
|---|
| باشتقاق طرفي المعادلة بالنسبة إلى س، ينتج أنّ: -جا(س ص)×(س(دص/دس) ص)=1 -س جا(س ص)×(دص/دس)=1 ص جا(س ص) دص/ دس=(1 ص جا(س ص))/(-س جا(س ص)) دص/دس=-(1 ص جا (س ص))/(س جا(س ص)) |







