بحث عن المتجهات

الكميات الفيزيائيّة

في الفيزياء توجد كميّات فيزيائيّة عديدة، بعضها تحتاج إلى تحديد مقدار هذه الكميّات، ويكون هذا كافياً للتعبير عنها بشكلٍ كامل، وبعضها تحتاج للتعبير عن مقدار هذه الكميّة واتجاهها، وهذا التنوع في الكميات الفيزيائيّة أمرٌ مهمٌّ جداً في الفيزياء؛ فالفيزياء هي إحدى العلوم الطبيعيّة، والتنوع في كمياتها مهمّ لوصف الطبيعة بشكلٍ صحيحٍ وشامل.

والكميات القياسيّة هي الكميات الفيزيائيّة التي تحتاج إلى مقدار فقط، ولا تحتاج إلى اتجاه للتعبير عنها، ومن الأمثلة عليها درجة الحرارة، والحجم ، والكتلة ، والطاقة، والكثافة، والضغط، وغيرها، لكن في المقابل، تحتاج الكميات المتجهة إلى تحديد كُلٍّ من المقدار والاتجاه لها حتّى يتم التعبير عنها، ومن الأمثلة على الكميات المتجهة القوة ، والوزن، والسرعة، والتسارع ، والزخم الخطي، والإزاحة، وغيرها؛ فعلى سبيل المثال، لو كان في سلّة بعض ثمار من التفاح ، وكان عددها عشر ثمارٍ مثلاً، فإنّ جملة (السلة تحتوي على عشر تفّاحاتٍ) كفيلةٌ بتوضيح الأمر، ولم يكن هناك داعٍ لتحديد الاتّجاه، وهذا أحد الأمثلة على الكميات القياسيّة، بينما لو قيل إنّ سرعة سيّارة هي 50 ميلاً في الساعة، فحينها يجب ذكر الاتّجاه أيضاً حتّى يكون الوصف متكاملاً وأكثر دقّةً.

عند المقارنة بين أيّ كميّتين قياسيّتين، فمن السهل المقارنة بين مقدار كلٍّ منهما، وإجراء العمليات الحسابيّة عليهما، بينما يكون الأمر أكثر تعقيداً في حال المقارنة بين كميّتين متّجهتين؛ وذلك لأنّ لكلٍّ منهما مقداراً واتّجاها، وعليه فإنّه يجب النظر في اتجاه كلٍّ منهما عند إجراء أيّ عمليّات حسابيّة عليهما؛ من جمع وطرحٍ وضربٍ وغيرها.

مركّبات المتّجهات

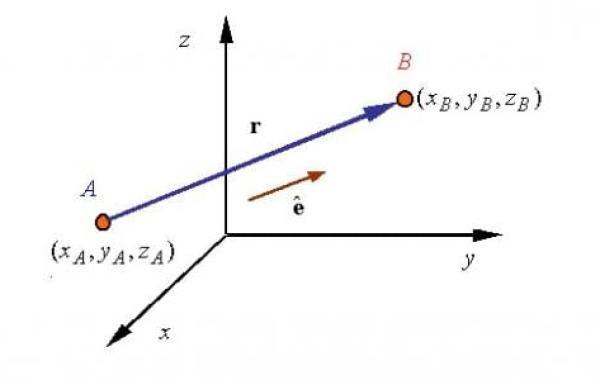
لأيّ مُتّجه توجد مُركبات تعتمد على نظام الإحداثيات الذي نحن فيه، وفي هذا المقال سيتمّ تناول نظام الإحداثيات الديكارتي، يمكن التعبير عن جميع المتجهات في المستوى الديكارتي من خلال مركبات سينيّة وصاديّة وعينيّة، حيث إنّ أي متجه يساوي مجموع هذه المركبات الثلاثة، أي المركبة السينيّة مضروبةً بمتجه الوحدة السينيّ، والمركبة الصاديّة مضروبة بمتجه الوحدة الصادي، والمركبة العينيّة مضروبة بمتجه الوحدة العيني، والمركبة هي تعبير عن طول المتجه على محاور نظام الإحداثيات المستخدم، فيمكن القول إنّ طول المتجه على محور السينات يساوي المركبة السينيّة لهذا المتجه، والأمر نفسه فيما يخصّ المركبتين الصاديّة والعينيّة.

كما ذُكِر سابقاً فإنّ متجه الوحدة يظهر عند التعبير عن المتجهات باستخدام المركبات، ويمكن تعريف متجه الوحدة على أنّه متجه عديم الأبعاد مقداره واحد، واتجاهه يُعبّر عن اتجاه كل مركبة من مركبات المتجه، وتخلتف متجهات الوحدة باختلاف نظام الإحداثيات المُستخدَم، ولو كان لدينا متجه في المستوى السيني والصادي فقط، ولو كانت الزاوية بين محور السينات والمتجه هي (φ)، فإنّ مقدار المركبة السينيّة سيكون مساوياً لطول هذا المتّجه مضروباً بجيب التمام للزاوية (φ)، وطول المركبة الصاديّة سيكون مساوياً لطول المتجه مضروباً بجيب الزاوية (φ).

خصائص الكميّات المتّجهة

للكميات المتجهة العديد من الخصائص، وخصائص هذه الكميات أكثر من خصائص الكميات القياسيّة كون الكميات المتجهة تحتاج إلى مقدار واتجاه ليتم التعبير عنها، لكن قبل البدء بالحديث عن خصائص المتجهات فلا بُدّ من توضيح أنّه يتم التعبير عن المتجهات -في بعض الحالات- باستخدام الأسهم، بحيث يُعبّر طول السهم عن مقدار هذا المتجه، بينما الاتجاه الذي يُشير إليه فإنّه يُعبّر عن اتجاه هذا المتجه، ومن خصائص هذه المتجهات:

• تساوي المتجهات: يكون المتّجهان متساويين فقط إذا كانا يمتلكان نفس الطول أي المقدار نفسه، ويُشيران إلى الاتجاه نفسه أي لهما نفس الإتجاه، فعلى سبيل المثال: يمكن القول إنّ متجهين يُشيران إلى الشمال ومقدار كلٍّ منهما 5، إذاً، هذان المتجهان متساويان، لكن لو كان لأحدهما مقدار مختلف أو يشير إلى اتجاه آخر كالشمال الشرقي على سبيل المثال، فإنّ هذين المتجهين لن يكونا متساويين.
• جمع المتجهات: يمكن جمع المتجهات عن طريق جمع مُركّبات المتّجه معاً؛ أي جمع المركبات السينيّة، وجمع المركبات الصاديّة، وجمع المركبات العينيّة كلٌّ على حِدة، أو يمكن جمع المتجهات بطريقة هندسيّة؛ بحيث يوضَع المتجه الأول ثمّ يوضَع ذيل المتجه الثاني على رأس الأول، وهكذا، وفي النهاية يُرسَم سهم من ذيل المتجه الأول إلى رأس الأخير، ويكون حاصل الجمع هو هذا المتجه الأخير الذي تمّ رسمه، وهو ما يُعرَف بالمتجه المُحصّل، ويخضع جمع المتجهات للخاصيّتين التبديليّة والترابطيّة للجمع.
• المُتّجه السالب: لو كان لدينا المتجه (A)، فإنّ المتّجه السالب منه هو المتجه الذي يُعطي صفراً عند جمعه مع المتجه (A)، وللمتجه السالب نفس مقدار نسخته الموجبة، ولكنّه يكون في الاتّجاه المعاكس له؛ أي أنّ بينهما 180°.
• طرح المتّجهات: عمليّة الطرح في المتجهات هي نفسها عمليّة الجمع، ولكن بدل جمع متّجهين فإنّه تتمّ إضافة المتجه الأول إلى سالب المتجه الثاني؛ أي إضافة المتجه الثاني بعد عكس اتجاهه.
• ضرب متّجه بكميّة قياسيّة: عمليّة ضرب المتّجه بكميّة قياسيّة هي ليست إلا تغييراً لطول المتجه، أي تغييراً لمقداره؛ أمّا اتّجاهه فلن يتغيّر إذا تمّ ضربه بأيّ رقم.
• ضرب المتّجهات ببعضها البعض: يوجد نوعان من الضرب عند الحديث عن ضرب المتّجهات؛ فعند ضرب متجهين ضرباً نقطياً، فإنه ستنتج كميّة قياسيّة؛ ولهذا يُعرَف هذا الضرب بالضرب القياسيّ، بينما إذا تمّ ضرب متجهين ضرباً تقاطعياً، فإنّ الناتج سيكون متجهاً جديداً عمودياً على كلا المتّجهين اللذين تمّ ضربهما؛ ولهذا يُعرَف هذا الضرب بالضرب الاتّجاهي.