ارتفاع المعين
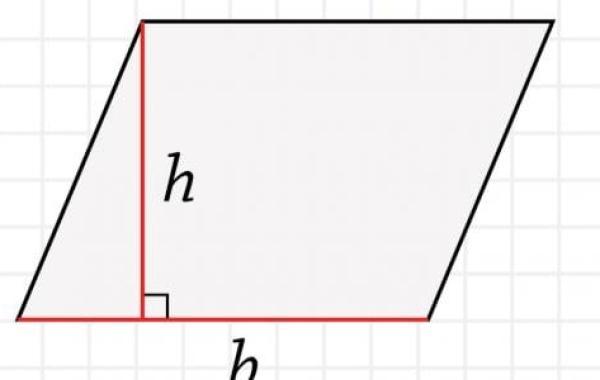
تعريف ارتفاع المعين
يُعرف ارتفاع المعين (بالإنجليزية: Rhombus Height) بأنه المسافة العمودية الواصلة بين ضلعَي المعين المُتقابلين، وهو يصنع زاوية قائمة مع الضلعين، والمعين هو عبارة عن شكل رُباعي مُتساوي الأضلاع، كل ضلعين مُتقابلين فيه متوازيان، وكل زاويتين مُتقابلتين مُتساويتان، أما قُطرَا المعين فيتلاقيان في المنتصف ويصنعان زاوية قائمة عند نقطة التقائهما.
طرق حساب ارتفاع المعين
هناك العديد من الطرق لحساب ارتفاع المعين، ومنها:
باستخدام قانون المساحة
يمكن حساب ارتفاع المعين دائماً باستخدام المعادلة العامة لمساحة المعين والتي تربط بين مساحة المعين وارتفاعه وطول ضلعه، وذلك كما يأتي:
ارتفاع المعين = مساحة المعين ÷ طول ضلع المعين.
وبالرموز:
ع=م/ل
حيث أن:
- ع: ارتفاع المعين.
- م: مساحة المعين.
- ل: طول ضلع المعين.
فمثلاً لو كان هناك معين تبلغ مساحته 64سم، وطول أحد أضلاعه يساوي 8سم، فإن ارتفاعه يساوي: الارتفاع = المساحة÷طول الضلع= 64÷8= 8سم.
باستخدام قيمة طول القطر وطول أحد الأضلاع
يمكن أيضاً حساب ارتفاع المعين اعتماداً على قِيَم الأقطار، بالإضافة إلى طول أحد أضلاع المعين، وقيمة المساحة، وذلك باستخدام المعادلتين الآتيتين:
- حساب مساحة المعين اعتماداً على طول الأقطار: يمكن حساب مساحة المعين باستخدام القانون الآتي :
المساحة = (القطر الأول×القطر الثاني)÷2
وبالرموز:
م=(ق×ل)÷2
- حساب ارتفاع المعين كما سبق من القانون الآتي:
الارتفاع = المساحة ÷ طول ضلع المعين
وبالرموز:
ع=م÷ل.
مثال توضيحي: إذا كان هناك معين طول قطره الأول 4سم، والثاني 6سم، وطول ضلعه 2سم، فإن ارتفاعه يساوي:
- المساحة = (القطر الأول×القطر الثاني)÷2= (4×6)÷2=12سم.
- الارتفاع = المساحة ÷ القاعدة = 12÷2= 6سم، وبالتالي فإن ارتفاع المعين المُعطى يساوي 6سم.
باستخدام قانون المساحة وقياس إحدى زواياه
يمكن أيضاً حساب ارتفاع المعين اعتماداً على طول أحد أضلاعه، وقيمة المساحة، وقيمة إحدى زواياه، وذلك باستخدام المعادلتين الآتيتين:
- حساب المساحة من طول أحد الأضلاع، ومن جيب إحدى زاوياه: باستخدام القانون الآتي:
المساحة= (طول الضلع)×جا (أية زاوية كم زوايا المعين)
وبالرموز:
م=(ل)×جا (أَ).
- حساب ارتفاع المعين كما سبق: من القانون الآتي:
الارتفاع = المساحة ÷ طول ضلع المعين
وبالرموز:
ع=م÷ل.
أمثلة متنوعة حول حساب ارتفاع المعين
وفيما يأتي أمثلة متنوعة حول حساب ارتفاع المعين:
- المثال الأول: إذا كانت مساحة المعين 360سم²، ومحيطه 48سم، جد ارتفاعه.
- الحل:
- حساب طول الضلع أولاً بتطبيق قانون: محيط المعين=طول الضلع×4 ، 48=4×طول الضلع، ومنه طول الضلع=12سم.
- تطبيق قانون الارتفاع = المساحة ÷ القاعدة = 360÷12= 30سم، ومنه ارتفاع المعين=30سم.
- المثال الثاني: احسب ارتفاع المعين (أب ج د) الذي يتمثل بالعمود (دو) الساقط من الزاوية د نحو القاعدة (ب ج) إذا كان طول جميع أضلاع المعين=17سم، وطول (و ج)=8سم.
- الحل: بتطبيق قانون فيثاغورس على المثلث (دوج) قائم الزاوية في (و) ينتج أن: (دج)²=(دو)² (وج)²، أي أن: (17)²=(دو)² (8)²، ومنه (دو)=15سم، وهو الارتفاع.
- المثال الثالث: إذا كانت مساحة المعين 315سم²، ومحيطه 180سم، جد ارتفاعه.
- الحل:
- حساب طول الضلع أولاً بتطبيق قانون: محيط المعين=طول الضلع×4، 180=4×طول الضلع، ومنه طول الضلع=45سم.
- تطبيق قانون الارتفاع = المساحة ÷ القاعدة = 315÷45= 7سم، ومنه ارتفاع المعين=7سم.
- المثال الرابع: إذا كانت مساحة المعين 72سم²، وكان ارتفاعه يعادل نصف طول ضلعه، جد قيمة ارتفاعه، وقيمة طول الضلع.
- الحل:
- نفترض أن الارتفاع هو (ع)، أن طول الضلع هو (2ع)، ثم حساب طول الارتفاع أولاً بتطبيق قانون: الارتفاع = المساحة ÷ القاعدة، ع=72÷(2×ع)، ومنه ع=12سم؛ أي أن ارتفاع المعين = 12سم.
- حساب طول الضلع بضرب الارتفاع بالعدد 2، لينتج أن طول الضلع=2×12=24سم.